
Liczę sobie w exelu takie pierdołki.
I pierw robiłem bez żadnych przybliżeń, a potem to samo równanie liczyłem z liczbami lekko przybliżonymi i wyszła duża różnica wyników :/
Skąd taka rozbieżność?
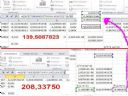
edit. Jak by co to 208 wychodzi na dole a 139 u góry :)
LOL
Jak to możliwe że podstawiając inną dane pod różową kratkę które są praktycznie takie same wychodzi zupełnie inny wynik czyli powyżej 200..
LOL
Odkryłem ze jeśli podstawię tylko liczbę 0,00025 a jak podstawię odnośnik do =0,015974937^2 to da inny wynik. LOL jak to możliwe ?
Coś niebieski komórki chyba nie tak są zaokrąglone.

Nie no kurwa jak to możliwe że kalkulator podaje jeszcze inny wynik?
Wpisałem dokładnie takie coś i wynik w kalkulatorze to 50,55....
Kurwa nie wyrobię całą noc się wczoraj z tym jebałem i od rana i nadal nie wiem o co chodzi :/
edit. a gdy w kalkulatorze zamiast ostatniego kwadratu dałem 0,00025 to wyszło 207
loool
Ja nie bardzo wiem o co Ci chodzi. Podstawiasz inne liczby to wychodzą inne wyniki. Tak ciężko to pojąć?
Może dlatego że zielona i fioletowa nie różnią się aż do 7 miejsca po przecinku a niebieska różni się na 5 i to aż o 2?
tomazzi podstawiając do tych równań raz jedno raz drugie niebieskie pole wynik ulegał nieznacznym zmianom.
A z tym 0,000255 to różnica od =0,015974937^2 to 1,98388504*10^-7 więc praktycznie to samo...
Ja jak wpisałem Twoje liczby (na tyle, na ile je widać na ekranie), to wyniki mi wyszły:
139,5329167
131,0913005.
A różnica bierze się właśnie z tych niewielkich różnic pomiędzy 0,000255 a wynikiem formuły. Weź pod uwagę, że masz w swojej głównej formule dzielenie przez "różnicę 5 pól zielonych i pola różowego". Wszystkie te liczby są bardzo małe, a zatem dzielisz przez liczbę bliską zera, bo posiadającą jakąś cyfrę różną od 0 dopiero na 7 miejscu po przecinku. Jeżeli teraz porównasz sobie wartości tej "różnicy..." dla konkretnej liczby oraz dla wyniku formuły, zobaczysz, że ta pierwsza jest trzy razy większa od drugiej!
liczba --> 3,29E-07
formuła --> 1,30388E-07
Tak więc wartość "pole niebieskie podzielić przez ta różnica" jest w przypadku liczby zaokrąglonej aż trzy razy większa. Stąd te duże rozbieżności. Operujesz po prostu liczbami tak bliskimi zera, że każda, choćby najmniejsza różnica wynikająca z zaokrąglenia, daje znaczącą różnicę w przypadku dzielenia przez tę liczbę.