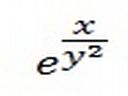
Matematyka
Jak można uprościć ten przykład, żeby policzyć pochodne? e^(x/y^2 )
Z góry proszę, by ktoś potwierdził to co napiszę, bo mogłem już zapomnieć jakichś niuansów związanych z liczeniem pochodnych funkcji.
Po co to w ogóle przekształcać?
Masz tu funkcję złożoną z dwóch części.
Pochodna z [e^(x/y^2)]' = [x/y^2]'+[e^(x/y^2)]'
[x/y^2]' to dzielenie, więc pamiętaj o odpowiednim wzorze na pochodną z dzielenia [x/y]' = (x'y-xy')/y^2.
Pochodna po x:
(y^2/y^4)e^(x/y^2)
czyli
(y^2)e^(x/y^2)
Pochodna po y:
-(2xy/y^4)e^(x/y^2)
czyli
-(2x/y^3)e^(x/y^2)
Czy ktoś mógłby to sprawdzić?
pierwsza pochodna z x: e^(x/y^2)*(1/y^2)
pierwsza pochodna z y: -(2x/y^3)*e^(x/y^2)
druga pochodna z x: e^(x/y^2)*(1/y^2) *(1/y^2)+ e^(x/y^2)*-(2x/y^3)
druga pochodna z y: e^(x/y^2)* -(2x/y^3) *-(2x/y^3)+ e^(x/y^2)*(-2x)*(-3y^-4)
pochodna mieszana: e^(x/y^2)*(1/y^2) *(1/y^2)+ e^(x/y^2)*-(2x/y^3)
A czy ten przykład mógłby ktoś sprawdzić?
u(x,y)=ln(e^x+e^y)
(d^2 u)/(dx^2 ) + du/dy =1 ?
du/dx=1/(e^x*e^y )*e^x= e^x/(e^x*e^y )
du/dy=1/(e^x*e^y )*e^y= e^y/(e^x*e^y )
(d^2 u)/(dx^2 )=(e^x*(e^x+e^y )-e^x*e^x)/(e^x*e^y )^2 = (e^x-e^x*e^x)/(e^x*e^y )
(e^x-e^x*e^x)/(e^x*e^y ) + e^y/(e^x*e^y ) =/=1
L=/=P