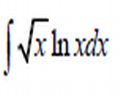
Taka całeczka
Niby prosta, a jednak ->
Podstawiam w ten sposób:
u= lnx
u'= 1/x
v'= x^(1/2)
v= 1/2 * x^(-1/2)
v obliczyłem ze wzoru: 1/n+1 * x^(n+1)
Odpowiedź jednak sugeruje żeby za v wziąć 2/3 * x^(3/2)
Co jest dla mnie nie zrozumiałe, bo:
Całka z x^(-1/2) = 1/(-1/2 + 1)* x(-1/2 +1)= 1/(1/2) * x^(1/2)= 2x^1/2
Czyli przed całkę wystarczy wstawić 1/2 tak jak ja zrobiłem w moim v i wtedy wyjdzie v'
Co robić?

Mi wyszedł taki potworek ->
Przyznam, że Twojego zapisu nie rozumiem.
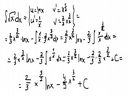
v jest równe całce z v', a z tego co widzę, to liczyłeś pochodną.
Edit: Tak powinieneś to zrobić.
Masz u, chcesz policzyć u', więc liczysz pochodną.
Masz v', więc żeby znaleźć v musisz policzyć całkę.
To dzięki, bo mi bardzo pomogłeś- myślałem, że całka z v ma dać v', a to na odwrót ;)
Całki fajna sprawa, jak się zna różne triki, to prościucha nawet.
Ale to jest dobre na hobby, jak kostka rubika. Odkąd zdałem egzamin z analizy matematycznej nigdy całka nie była mi potrzebna w zawodzie ;)