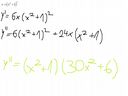
Jak obliczyć pochodną drugiego rzędu tej funkcji? ->
Pierwszą pochodną obliczyłem korzystając ze wzoru x^n= nx^(n-1)
gdzie moim x był nawias (x^2 +1).
Więc wyszło mi 3(x^2 +1)^2 i jeszcze pomnożyłem to przez pochodną tego (x^2 +1).
Czyli pod koniec miałem taki wynik 3(x^2 +1)^2 * 2x = 6x(x^2 +1)^2
I z tego starałem się obliczyć pochodną drugiego rzędu:
6x(x^2 +1)^2
Za pomocą wzoru na mnożenie f'(x)*g(x) + f(x)*g'(x)
gdzie moim f(x) było 6x,
a g(x) było (x^2 +1)^2.
Oczywiście pochodną -g'(x)- rozłożyłem za pomocą wzoru na x^n.
A następnie drugą część [f(x)*g'(x)] pomnożyłem jeszcze przez pochodną (x^2 +1), czyli 2x.
Więc na końcu miałem:
6(x^2 + 1)^2 + 6x*2(x^2 + 1) * 2x
Ale jak widzicie wynik ten się nie zgadza z prawidłowym wynikiem- który zapisałem na zielono.
Jak Wy byście to zrobili? W obliczaniu pochodnej drugiego rzędu użylibyście innego wzoru?

Opisowe wyjaśnienie może być zbyt niezrozumiałe- więc tutaj zdjęcie ->
(białe pola żeby zmieścić się w maksymalnym rozmiarze pliku).
Przecież twój wynik jest równy poprawnemu - wystarczy przekształcić wyciągając x^2+1 przed nawias
zielony wynik jest ok, jak Ci juz napisal wyzej , ale mozesz zostawic w postaci ktora masz, to nie jest blad.elegancki zapis to ten zielony ale Twoj tez ok.