Wiem, że jest pełno odpowiedzi na te zadania, jednakże chciałbym poznać sposób jak szybko rozwiązywać tego typu zadania. Akurat nie było mnie w szkole kiedy były te zadania przerabiane i nie wiem jak się do tego zabrać, tak aby było poprawnie i szybko wykonane.
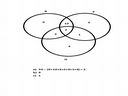
zadanie przerabiane w szkole (rozwiązanie na obrazku)
W klasie Ib jest 34 uczniów, wśród których: 24 umie jeździć na rowerze, 16 umie pływać, 10 umie jeździć na nartach; w tej liczbie 12 umie pływać i jeździć na rowerze, 5 umie jeździć na rowerze i na nartach, 3 umie pływać i jeździć na nartach. Dwie osoby w Ib uprawiają wszystkie wymienione dyscypliny sportowe.
a) Ile osób w klasie Ib nie uprawia żadnej dyscypliny sportowej?
b) Ile osób umie tylko jeździć na rowerze?
c) Ile osób umie tylko pływać i jeździć na nartach?
Gdy mam już zrobiony rysunek pomocniczy nie ma problemu, żeby odpowiedzieć na pytania, jednakże chciałbym się dowiedzieć jak taki rysunek zrobić, skąd mam wiedzieć gdzie wpisać 9, 10, 3, 2 itd...?
Looooooool zbiory, która to klasa. 1 gimnazjum?
Chyba, że nowy program jest znowu głupszy niż to co było.
Zbiory były w 3 gim, ja jestem w 1 LO. W gimnazjum było tylko 1 takie zadanie przerabiane :D Akurat z wszystkiego co do tej pory przerabiałem z matematyk to właśnie zbiorów nie lubię.
[3] Czyli miałem rację, nowy program.
Skończ ze sobą proszę jeżeli nie potrafisz tak prostego zadania zrobić
Ciekawt Fryzjer - taki mądry jesteś to wyjaśni dlaczego tak, a nie inaczej zostały przedstawiony liczby na rysunku. Zadanie może bym zrobił po 15-20min, niestety na kartkówce, sprawdzianie tyle czasu nie mam.
a) Dodajesz wszystkie wartości, które są w kółkach i odejmujesz od liczby. Na szybkiego wyszło mi 34 -32 = 2. Czyli dwie osoby nie uprawiają żadnych sportów, mogę się mylić ;)
b) 9 osoby umie tylko jezdzic na rowerze, wyczytujesz z tabelki.
c) 3 + 4 = 7
z tego co pamiętam zbiory zapisywalo sie w taki sposób :
R = ‹ jakaś wartość›
Dla zadania trzeciego będzie to:
R, N = ‹ 3 , 4 ›
Problem z wytłumaczeniem tego zadania polega na tym, że jest to bardzo podobne do tłumaczenia dlaczego klocek w kształcie kwadracika trzeba włożyć w kwadratową dziurkę (czyli: tak proste, że nie wiadomo w czym może tkwić problem). No ale ok, spróbujmy:
Każde z tych kółek reprezentuje podzbiór uczniów, którzy uprawiają daną dyscyplinę sportu (oczywiste - tłumaczyć chyba nie trzeba). Żeby się nie pomylić zostały podpisane pierwszymi literami nazw dyscyplin ;)
Z treści zadania wynika, że w zbiorze (znaczy w kółku) rowerzystów (czyli "R") mają być w sumie 24 osoby (czyli wszystkie liczby jakie tam wpiszemy mają się sumować do 24). Z kolei w zbiorze pływaków, ma być w sumie 16, a w narciarzach 10. Ponadto wiemy, że jest 12 "pływako-rowerzystów", czyli w tej migdałowatej "łezce" będącej częścią wspólną zbiorów P i R ma być w sumie 12 osób. Analogicznie - w łezce wspólnej dla R i N ma być 5 osób, a w części wspólnej dla P i N mają być 3 osoby. Na koniec wiemy, że wszystkie dyscypliny sportu uprawiane są przez 2 osoby, czyli w tym okrągło-trójkątnym czymś po środku ma być wpisane 2.
Teraz "cofając się" w powyższych danych wpisujesz odpowiednie liczby - najpierw do "łezek" będących częścią wspólną każdej pary zbiorów (ale już POZA tym środkowym "trójkącikiem" bo tam już jest 2 uczniów, co to wszystko umieją). A więc w "łezce" P i R ma być wpisane 12-2=10, w "łezce" R i N ma być 5-2=3, a w "łezce" P i N ma być 3-2=1 (to "-2" wszędzie się bierze stąd, że w łezce ma być W SUMIE iluśtam uczniów, ale z tego odejmujemy 2, których już uwzględniliśmy w "trójkąciku" wspólnym dla wszystkich sportów). Teraz wiedząc ile jest w tym środkowym "trójkąciku" i każdej "łezce" możesz z łatwością policzyć ile ma być wpisane w pozostałych "dużych" częściach każdego koła. Na sam koniec sumujesz sobie wszystkie wpisane liczby otrzymując informację ilu uczniów W OGÓLE uprawia JAKIKOLWIEK sport (lub sporty), a stąd już łatwo policzyć ilu nie uprawia ŻADNEGO.
Akurat nie było mnie w szkole kiedy były te zadania przerabiane i nie wiem jak się do tego zabrać, tak aby było poprawnie i szybko wykonane.
Rób zadanie "od końca".
