

GOL-owy kalkulator, czyli - Matematyka - Królowa wszystkich nauk. Cz.10
Wątek ten poświęcony jest przede wszystkim wspólnej pomocy w rozwiązywaniu zadań matematycznych.
-------------------------------------------------------------------------------------------------------------
Regulamin:
- Piszemy tutaj tylko i wyłącznie zadania matematyczne (czyt. nie zbaczamy na na tematykę innych przedmiotów itd.) oraz odpowiedzi na konkretne np. równanie.
- W swych wypowiedziach zważamy na wszelkie znaki interpunkcyjne oraz ogólną logikę zdań.
- Wypowiadając się nie używamy wulgaryzmów oraz obraźliwych zwrotów w stosunku do innych użytkowników forum.
-------------------------------------------------------------------------------------------------------------
Polecana NOTACJA matematyczna:
Podstawowe symbole
+ - dodawanie
- - odejmowanie
* - mnożenie
/ lub ewentualnie : - dzielenie
^ - potęgowanie
Przykład: 3^(x-2)
sqrt() - pierwiastek kwadratowy (drugiego stopnia)
Przykład: 2+sqrt(3)
sqrt[n]() - pierwiastek n-tego stopnia
Przykład: 5-2*sqrt[3](7) ("pięć minus dwa pierwiastki sześcienne (pierwiastki trzeciego stopnia) z siedmiu")
[] () - nawiasy w kolejności od najbardziej zewnętrznych. Polecamy jednak używać tylko nawiasów okrągłych () - również zagnieżdżając jedne w drugie - gdyż nie powoduje to niejednoznaczności, a nawiasy kwadratowe [] mogą także oznaczać część całkowitą liczby.
UWAGA! Pilnuj, aby każdy otwarty nawias miał swoje zamknięcie! W przeciwnym razie wyrażenie jest praktycznie nie do odczytania!
Przykład: 1/(1+1/(1+1/(1+1/(...))))
inf - symbol nieskończoności
Litery greckie i inne symbole specjalne można zapisywać słownie lub dowolnym znakiem pod warunkiem opisania co on oznacza!
Ułamki zwykłe
Należy używać nawiasów aby licznik i mianownik były jednoznaczne.
Przykład: (3+7x)/(2y-5)
Przykład: 3+7x/(2y-5)
Przykład: 3+7x/2y-5
Powyższe przykłady NIE SĄ tożsame!
Ułamki piętrowe
Tu również należy używać nawiasów.
Przykład: (3+7x)/(2y-5/(17+2*z))
Liczby mieszane
Dla jednoznaczności liczby mieszane typu 3 1/2 ("trzy i jedna druga") należy zapisywać jako sumę, np. (3+1/2) - często będzie konieczne ujęcie jej w nawias - lub ułamek niewłaściwy, np. 7/2. Preferowany jest jednak zapis w postaci ułamka dziesiętnego (tam gdzie to możliwe, tzn. gdy ułamek taki nie będzie miał nieskończonego rozwinięcia dziesiętnego)
Przykład: (3+1/2)
Przykład: 7/2
Przykład: 3,5
-----------------------------------
Powyższa notacja jest wzorowana na składni LaTeXa. Nie polecamy jednak stosowania tej składni w pełnej wersji - forum GOL nie obsługuje markerów TeXa i nie przetwarza formuł, które z kolei są trudne do czytania przez ludzi.
-------------------------------------------------------------------------------------------------------------
Przydatne linki przy rozwiązywaniu zadań:
- http://www.matmana6.pl/
- http://www.poolicz.pl/
- http://www.obliczone.pl/
- http://www.wolframalpha.com/
- http://matematyka.pisz.pl/
-------------------------------------------------------------------------------------------------------------
Nowa część wątku zostanie utworzona po przekroczeniu 200 postów.
-------------------------------------------------------------------------------------------------------------
GOL-owi matematycy:
- lajtowy ziomek:) | Ogólnie: zakres wiedzy obejmujący materiał do klasy 3 Liceum. Chętnie pomogę z funkcji kwadratowej oraz wszelkich równań, nierówności. Słabość - Geometria. :P
- Filevandrel | Cały materiał LO i materiał z 2 lat studiowania elektroniki, łapać na maila [email protected] zawsze chętnie odpiszę!:)
- tomazzi | podstawówka, gimnazjum, liceum, co nie co ze studiów. Lubię zadania na rozkminkę :P
- DEXiu | cały zakres do szkoły średniej włącznie; matematyka "wyższa" na poziomie studenta uczelni technicznej (nie matematyki na uniwerku:) - mat. dyskretna, geometria, analiza, algebra, statystyka, probabilistyka; bardzo chętnie zadania i zagadki logiczne
- Maco | Zakres do LO i troszkę matematyki wyższej | Pięta achillesowa - trygonometria
- $ebs Master | Zakres - liceum, studia bez prawdopodobienstwa
- Łysy. | Cała rozkminka aż do liceum, szczególnie lubię geometrię. Potem analiza, algebra, podstawy dyskretnej, podstawy probabilistyki.
- Mathmi Thenthur | matematyka na poziomie szkoły średniej plus studia ekonomiczne: analiza, algebra, statystyka, rachunek prawdopodobieństwa; wybitnie nie lubię geometrii
- jagged | Zakres szkoły średniej + semestr informatyki na EAIiE (AGH) + wciąż studia informatyczne na Politechnice
-------------------------------------------------------------------------------------------------------------
Linki do bannerów:
- http://img685.imageshack.us/img685/9937/bannermatematyka.jpg ~by A's
- http://img232.imageshack.us/img232/9959/bannerme.png ~by lajtowy ziomek
- http://img842.imageshack.us/f/matma2j.jpg/ ~by A's
-------------------------------------------------------------------------------------------------------------
Poprzednia część:
https://www.gry-online.pl/forum/gol-owy-kalkulator-czyli-matematyka-krolowa-wszystkich-nauk-cz9/zfabd305?N=1
dla jakich wartości parametru m równanie ma dwa różne rozwiązania??
(m+2)x²-2x+m+2=0
(chodzi mi o to jak policzyć początkową delte)
(chodzi mi o to jak policzyć początkową delte)
tak jak zwykle, wg wzoru delta=b^2-4ac, tyle że wartości a b c będa zawierać parametr m.
Otrzymasz w ten sposób wyrażenie z wartością m, które musisz przyrównać do >0 =0 <0.
Dwa różne rozwiązania będziesz mieć dla delta>0, ale to już powinieneś mieć w małym palcu :)
Potrzebuje pomocy z rozlozeniem wielomianu
x^2 (x^2 +5)- x^2(x^2-5)
widze kawalek wzoru skroconego mnozenia ale nie abrdzo wiem jak to zrobic :S (bo roznica)
[4] Możesz wyciągnąć z każdego składnika x^2, otrzymasz wtedy:
x^2 * (x^2+5-x^2+5) = 10*x^2
[5] 5) Jedyne co mi przychodzi do głowy to zapisanie ułamka w postaci iloczynu dwóch ułamków - licznik i mianownik z siódmą potęgą oraz 1/(4+4*sqrt(3)*i)^2. Potem pozbycie się "i" z mianownika pierwszego ułamka - pomnożenie go przez sprzężenie mianownika. W liczniku dalej zostaną duże liczby, ale będzie to już tylko mnożenie, a ten drugi ułamek też już prosty.
9) Mnożysz przez sprzężenie mianownika i dochodzisz do postaci: (10-10i)^7.
moglby ktos mi pomoc? bo juz nie pamietam praktycznie nic z ciagow a potrzebuje jak sie znajduje wzor ciagu liczbowego
przykladowo mam:
6
12
24
48
czy jest jakis ogolny sposob jak znalezc wzor czy to jest tylko "na zgadywanie"?
Raczej na zgadywanie.
a moglbys pomoc z tym ciagiem co podalem?
Szukasz sobie zależności pomiędzy sąsiednimi elementami. Np.: 6 i 12, 12 i 24. Jak się da łatwo zauważyć w obu przypadkach, kolejny element jest 2 razy większy od poprzedniego. 12/6=2, 24/12=2. Tak więc wzór na n-ty element to: a(n) = 2* a(n-1) czyli element n-ty to 2* element o indeksie n-1.
a czym tutaj we wzorze jest "a"?
aha, zapomnialem o najwazniejszym czyli pierwszym wyrazie ciagu ktory wynosi 3
a to element. a1 to pierwszy element(wyraz) ciągu czyli 3, a2=6, a3=12 itd. Jeżeli chcesz obliczyć 17 wyraz ciągu to: a17 = 2 * a16
ale chodzi mi o wzor ogolny na kazdy element bo na obliczanie kolejnych to mialem juz podany
Nawet nie raczej, tylko NA PEWNO "na zgadywanie", bo (tak z formalnego punktu widzenia) skończona liczba podanych wyrazów ciągu definiuje nieskończenie wiele pasujących "wzorów". Zwykle więc chodzi o to, żeby "zgadnąć" (wymyślić) najprostsze i najlogiczniejsze wytłumaczenie (w stylu: "każdy wyraz jest dwa razy większy niż poprzedni", "każdy wyraz jest sumą dwóch poprzednich" itp. :)
EDIT: To trzeba było od razu mówić. Tym bardziej, że pewnie nie chodzi o zagadki typu: podane kilka wyrazów ciągu - odgadnij zasadę, a o zwykłe szkolne zadania z ciągu arytmetycznego i geometrycznego :/
Ogólny wzór Twojego ciągu: a_n = 3*2^(n-1)
a(n) = 2^n + 2^(n-1)
a wiec moglbys przytoczyc wzor ogolny tego ciagu? bo na an+1 to wiem ze jest rowny 2n ale potrzebuje ogolnego wzoru ciagu
EDIT
dzieki wam
Shog - Wyciągnij minus przed ułamek (tylko po to, żeby sobie odwrócić kolejność w liczniku i lepiej widzieć ;) ), mianownik rozłóż ze wzoru na różnicę sześcianów i skróć.
Wielkie dzięki DEXiu :)
Jeszcze jeden pewnie banalny przykładzik z którym mam problem.
lim
x->5
2x^2-11x+5/3x^2-14x-5
Ok zrobiłem. Reguła l'Hospitala.
[inf]<=>nieskończoność
[inf=x]<=>nieskończona ilość x
1-0,(9)=0,0[inf=0]1. To dowód, że 1-0,(9) NIE jest równe 0.
Wielu pewnie powie, że to herezje, lecz to prawda. Pogódźcie się z tym i już. ;)
Kto się nie zgadza, może oczywiście to (nieudolnie) udowodnić... :P
Może ktoś poradzić, jak najlepiej obliczać całki, które mają w mianowniku e^x?
mineral ---> Aż tak biegły w całkach nie jestem, żeby bez zobaczenia konkretnego przykładu podać rozwiązanie :p A tak bardziej serio to podaj przykład a łatwiej będzie pomóc.
Shoggoth ---> Na przyszłość zadaj chociaż pytanie lub powiedz z czym masz problem. I nie zapominaj o znaku = w przykładach, które zamieszczasz.
No np. całka z ( x^2 dx )/e^x
Bliska mi osoba już śpi więc żeby jej nie obudzić nie będę już dzisiaj tłukł w klawiaturę. ograniczę się do wklejenia linka. Klikasz - show steps i Ci wszystkie kroki ładnie pokaże. Jak czegoś nie będziesz rozumiał to pisz. Jutro ja(albo ktoś inny) na pewno Ci pomoże. Dobranoc ;)
http://www.wolframalpha.com/input/?i=integral%28%28+x%5E2+dx+%29%2Fe%5Ex%29
dla jakich wartości parametru m równanie ma dwa różne rozwiązania
mx^2 -(m+1)x -2m+3=0
delta >0
Cześć. Muszę narysować w jednym układzie współrzędnych wykresy funkcji:
f:x->4
g:x->2x-4
Problem polega na tym, że nie miałem jeszcze takiego zapisu funkcji i nie wiem o co w tym chodzi. Możecie mi jakoś to wytłumaczyć? Drugi problem polega na narysowaniu tej figury w symetrii względem osi x, bo nie wiem jak to narysować.
[30] Chodzi chyba o to, że fcja f przekształca x w 4, czyli będzie to po prostu pionowa linia na punkcie 4, a fcja g przekształca x w 2x-4, czyli wykresem będzie fcja 2x-4. Teraz jeśli masz narysować to na jednym układzie współrzędnych, to otrzymasz figurę ograniczoną wykresami tych dwóch fcji oraz osią x. Odbicie polega na przerysowaniu lustrzanie tych wykresów pod osią x.
help z wielomianów
http://imageshack.us/photo/my-images/600/img1105bw.jpg/
zad od 2.6 do 2.16 wskazówki sposoby rozwiazan (bez używania pochodnych) cokolwiek
Wspolrzedne wektora mowia tylko o jego dlugosci, a nie chociazby o polozeniu jego poczatku w ukladzie wspolrzednych. Wiec po co nazywac to wspolrzednymi?
[32]
2.6 Dzielisz jeden wielomian przez drugi - reszta, którą otrzymasz ma być równa 0.
2.7 Skoro jest podzielny to znaczy, że reszta z tego dzielenia jest równa 0 - tak otrzymasz współczynniki a i b. Potem wykonujesz zwykłe dzielenie w(x) przez podany dwumian.
2.8, 2.9, 2.10 Patrz 2.6.
2.11 Podnosisz drugi wielomian do kwadratu i porównujesz współczynniki przy odpowiednich potęgach x.
2.12 To wydaje się być skomplikowane, chyba że znajdziesz od razu takie współczynniki p i q, że równanie to będzie można sprowadzić do postaci kwadratowej. Żmudniejszą drogą jest zauważenie, że skoro istnieją 4 rozwiązania z czego 2 się powtarzają, to można ten wielomian zapisać jako: (x-x1)^2 * (x-x3)^2. Wszystko wymnażasz i otrzymujesz układ równań, dzięki któremu z 2 pierwszych równań znajdujesz pierwiastki wielomianu, a z 2 kolejnych szukane współczynniki.
2.13 Patrz 2.6.
2.14 Nie pamiętam tych wzorów na dzielenie wielomianów z resztą. Ale ułożysz kilka równań i powinno coś wyjść, a jak nie to zakładasz, że wielomian w jest jakiś tam i dzielisz po kolei przez te podane wielomiany, żeby otrzymać daną resztę - na podstawie tego wyznaczasz współczynniki i na koniec dzielisz przez ostatni wielomian i masz resztę.
2.15 Fajne zadanie. Przenosisz wszystko na jedną stronę i dochodzisz do punktu, gdzie musisz wykazać, że wielomian 4-stopnia jest większy lub równy 0. Ja pogrupowałem go w ten sposób: x^2 * (x^2-6x+5) + 4 * (2x^2-3x+1). Teraz zauważam, że pierwiastkami lewego trójmianu są 1 i 5, a prawego 1 i 1/2 - mogę więc wyciągnąć z obu składników (x-1). Otrzymuję: (x-1)(x^3-5x^2+8x-4), po znalezieniu pierwiastków wielomianu 3-stopnia, dostaję ostatecznie: (x-1)^2 * (x-2)^2, a iloczyn kwadratów jest zawsze większy lub równy 0. Prościej - strzelasz, że pierwiastkiem początkowego wielomianu jest jedynka, więc możesz go podzielić przez (x-1). Potem znów strzelasz i znów trafiasz, że jest jedynka - dzielisz. Potem strzelasz jeszcze dwa razy, trafiasz w dwójkę, dzielisz i po zadaniu.
2.16 Liczysz deltę, rozpatrujesz 3 przypadki i na tej podstawie wyznaczasz współczynnik.
EDIT: NIEWAŻNE (Proszę o usunięcie postu, gdyż prośba jest już nieaktualna, sam doszedłem do sedna sprawy)
predatronix (edit posta [35]) ==> To już nie pierwszy raz, kiedy taka sytuacja się zdarza. Następnym razem zadawaj pytanie na forum po 5 GODZINACH intensywnego myślenia nad problemem a nie 5 sekundach :/
2.6 - nie znam x dla ktorego reszta jest rowna 0 ( wielomian drugi nie ma pierwiastkow)
2.9 - niewykonalne bo z dzielenia i podstawiania 1 do wielomianu wychodzi to samo równanie.
2.12 : nvm szkolny blad przy potegach wychodzi juz
2.16 : wielomian 3-go stopnia. wiec delta odpada, robiłem to podstawiajac najpierw za m=0 potem m=4 , dla pozostałych liczb wychodzi tożsamość ze f(2)=0.
xkxtx
2.6 - ale jakie to ma znaczenie czy drugi wielomian ma pierwiastki? Masz oba te wielomiany podzielić pisemnie, dostajesz jakiś iloraz (wielomian stopnia drugiego) i resztę (dwumian pierwszego stopnia o współczynnikach zależnych od p i q). I ta reszta ma być TOŻSAMOŚCIOWO równa 0, czyli równa 0 dla każdego x (taką równość tożsamościową oznacza się znakiem równości o trzech kreskach (jak przystawanie), ale to szczegół).
2.9 - ???
Ja mam pytanie dotyczące pewnego doświadczenia z fizyki. Nie chciałem tylko dla niego zakładać wątku, więc:
do naczynia (szklanki) nalewana jest woda do pełna. Z góry nasuwane jest płaskie zamknięcie, w ten sposób, aby nie powstał bąbelek powietrza w środku. Naczynie jest odwracane i zamknięcie nie spada na dół. Do tego miejsca wszystko jest dla mnie jasne, ale potem zamknięcie jest zsuwane i woda się nie wylewa, tylko "wisi" w powietrzu. Może mi ktoś wyjaśnić jakie siły tutaj działają?
Dosyć szczegółowo opisane powyższe zjawisko.
A ja mam dosyć proste przykłady, ale chciałbym aby mnie nakierowano. Chodzi o zadanie: "Rozwiąż metodą graficzną podane układy równań" Mam 4 układy, ale chcę tylko 1, aby mi ktoś pomógł i nakierował.
y=2x-3
y=12-x
I co tu dalej z tym zrobić? Czy może po prostu narysować tabelkę, powymyślać jakieś x, podstawić je za te w układzie i rozwiązywać? To o to chodzi?
Tak jak wspomniałeś:
- robisz tabelkę
- na jej postawie rysujesz wykresy
- z układu współrzędnych odczytujesz punkt/punkty przecięcia funkcji, które są rozwiązaniem
dla jakich wartości parametru m , każdy z dwóch różnych pierwiastków równania x^‹2› -6mx- 2- 2m +9m^‹2 jest większy od 3
delta>0
f(3)
xw>3

Kurczę akurat szukałem tego tematu. Założyłem nowy. Ale no cóż, tutaj też się spytam.
https://www.gry-online.pl/forum/trudne-zadanie-z-matematyki/z3b2c471?N=1
Wiem, że był gdzieś seryjny wątek o takich problemach, ale nie mogę go znaleźć. Jest to zadanie ze skali podobieństwa. Czyli są dwie figury, o podanych polach (P1 i P2) i trzeba tą skalę obliczyć (powiedzmy 1:3). Wzór to P1*P2=K do kwadratu . Akurat nie wiem jakie on ma zastosowanie w tym zadaniu, no ale trudno...
"Stosunek pól dwóch trójkątów równobocznych wynosi 1 do 9 (1/9) . Oblicz długości boków tych trójkątów, jeżeli pole jednego z nich jest równe [tutaj odsyłam do obrazka po prawej] cm kwadratowych. Rozważ wszystkie przypadki"
Z tyłu książki są dwa wyniki, ale nadal z nich nic nie wychodzi. Wyszło im:
1cm i 3cm
lub
3cm i 9cm
Wie ktoś jak to rozwiązać? Byłbym bardzo wdzięczny za odpowiedź.
1/3= P1*P2
no i w jednym przypadku podstawiasz pod pole pierwszego ta dana, a w drugim pod pole drugiego i masz dwa przypadki
a potem boki wyliczasz z wzoru na pole trojkata rownobocznego czyli P=a^2 sqrt3/4
przynajmniej tak mi sie wydaje, sprobuj
należy skorzystać ze wzoru na pole trójkąta równobocznego.
http://matematyka.pisz.pl/strona/856.html
no i jeśli wiesz, że stosunek pól wynosi 1/9 to rozważasz dwa przypadki:
a) podane pole powierzchni jest trójkąta większego
b) podane pole powierzchni jest trójkąta mniejszego
^ valem i browar - coś mi świta, ale po długich bojach z mojego mózgu nic nie zostało. Przełomem okazał się wzór na pole. Rzeczywiście, identyczne jak w zadaniu. Zamiast a jest tylko 9.
Problemem jest tylko policzenie takiego pola... coś tam wymyślę.
dla jakich wartości parametru m , każdy z dwóch różnych pierwiastków równania x^2 -6mx- 2- 2m +9m^2 jest większy od 3
pomożecie mi napisać w tym założenia ??
[51]
po prostu podstawiasz dane pod wzor na pole i jedna niewiadoma jest bok trojkata, nic trudnego ;)
[52]
delta>0
a reszte sobie kombinuj, podpowiem, zrob przykladowy rysunek jak maja byc umiejscowione te pierwiastki, na pewno reszta Ci przyjdzie do glowy

Trzeba okreslic rząd macierzy w zaleznosci od parametru p. Oczywiscie zaczynam od policzenia wyznacznika, ktory nie chce mi za nic wyjsc tak jak w odpowiedziach (wszystko jest dobrze, oprocz tego, ze nie ma w odpowiedzi liczby -5, ani zadnej liczby oprocz wyrazen w nawiasach).
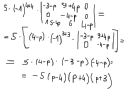
Rozwiazanie, korzystam z Laplace'a ->
Co jest nie tak?
Podejrzewam ze pomijane jest umyslnie cokolwiek poza nawiasami, bo jest niepotrzebne do okreslenia rzedu, no ale wole sie upewnic.
http://imageshack.us/photo/my-images/805/img20111116184049.jpg/
moglby mi ktos pomoc nad 2.113 i 2.115? glowie sie nad tym i glowie i mic iagle zle wychodzi....
prosze tylko o jakies naprowadzenie zeby,m wiedzial co dalej
[57]
2.113 x,y - boki przyprostokątne, z - bok przeciwprostokątny. 2y=x+z z założenia, że tworzą ciąg arytmetyczny. x^2+y^2=z^2 z założenia, że to trójkąt prostokątny. x lub y lub z = 30, musisz załóżyć, że któryś tam bok równa się 30 i podstawić do tych dwóch równań i masz układ 2 równań z dwiema niewiadomymi.
2.115 Znajdź wzory wiążące pole trójkąta opisanego na okręgu z promieniem tego okręgu + założenia jw.
[55]
Rząd macierzy to jest wielkość najmniejszej macierzy, dla której wyznacznik jest równy 0. detA dla macierzy 4x4 obliczyłeś dobrze - teraz porównujesz to do 0 i masz odpowiedzi: p=-4, p=-3, p=4 i dla tych p rząd jest równy 4. Teraz zakładasz, że p jest różne od tych trzech liczb i liczysz wyznacznik dla którejś macierzy 3x3 itd. itp.
jagged
co do 2.115 to wzor r=2pole/a+b+c chyba moze byc? wtedy dwiema niewiadomymi sa reszta i wyraz pierwszy, dobrze?
EDIT
juz wiem, niepotrzebnie podstawialem pod drugi i trzeci wyraz reszte i wyraz pierwszy, bede mial trzy rownania z trzema niewiadomymi, dzieki jagged
w 2.115 doszedlem do takiego ukladu
5b^2 - 4bc=0
b^2 - 1/2bc - 21b=0
jak to dalej rozwiazac?
juz dalem sobie, rade, przepraszam za klopoty
EDIT2
chociaz nie, bo ja zrobilem metoda przeciwnych wspolczynnikow i mi potem pole wyszlo ponad 1000, a powinno wyjsc 294, sam juz nie wiem.....
EDIT3
idiota ze mnie, zrobilem karygodny blad NA POCZATKU ukladu bo wzialem pod uwage 1/2 ktorej to liczby nie powinno byc, wyszlo ok, jeszcze raz dzieki jagged, wszystko ok ;)
Przepraszam za spam :)
Mam takie coś z wartości bezwzględnych:
||x-2|-4| < 2
|x-2| - 4 < 2 lub |x-2| - 4 > -2
|x-2| < 6 lub |x-2| > 2
już wyznaczyłem na osi te liczby etc, ale co mam dalej zrobić? Mam pewne wątpliwości co do prawej strony (|x-2| > 2) Jak wyznaczyć z tego te liczby większe?
preDratronIX --> Po pierwsze to nie spójnik "lub" (alternatywa) tylko "i" (koniunkcja). Dalej robisz tak samo - lewą nierówność znowu na koniunkcję dwóch nierówności, a prawą na alternatywę.
to wyszło mi
x>8 ^ x<-4
x<4 v x>0
i xE (8,+∞> u <-∞,-4)
xE [dla lewej strony] (0,4)
edit te "znaczki" to znak nieskończoności
Weź no to sprawdź jeszcze raz, bo żeby WSZYSTKIE kierunki nierówności na raz pomylić, to się rzadko zdarza :P Później połącz obie linijki spójnikiem "i" i wyciągnij wnioski jakie w końcu jest to x.
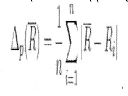
Przedmiot: fizyka
dział: prąd elektryczny, czyli oporność itp.
Mam taki wzór - napiszcie mi co za co podstawić, jak to zrobić.
[65]
Delta, czyli jakiś błąd jest do obliczenia. Znak sumy mam nadzieję rozumiesz, n - ilość pomiarów, R z kreseczką - opór średni, R - opór i-tego pomiaru.
[61]
||x-2|-4| < 2
|x-2|-2 < 2 i |x-2|-2 > -2
|x-2| < 4 i |x-2| > 0 (wartość bezwzględna jest zawsze większa od 0, wykluczamy tylko sytuację, gdy będzie równa 0, czyli x = 2)
x-2 < 4 i x-2 > -4 i x != 2
x < 6 i x > -2 i x != 2
Odp. xe(-2 ; 2)u(2 ; 6) albo jak kto woli: xe(-2 ; 6)\‹2›
Przez pomyłkę napisał.
Zrób tak jak pokazał tylko popraw ten błąd rachunkowy.
wie ktoś jak obliczyć granice:
cos (1/n)^2
oczywiscie przy x zmierzajacym do nieskonczonsci
Z góry dziekuje
Fabianos ==> Może z uwagi na późną porę czegoś nie dostrzegam, ale... ze względu na ciągłość funkcji cosinus możemy wciągnąć granicę pod nią i dostajemy:
lim cos(1/n)^2 = cos(lim (1/n)^2) = cos(0) = 1
Przy okazji: jeśli x zmierza do nieskończoności to granica będzie wynosiła cos(1/n)^2 bo tu nie mamy x ;)
28 - 7 = 15
Ludki kochane zamieńcie mi 3,(16) na zwykły mi wychodzi 313/99, a w odpowiedziach jest 313/90 nie wiem jakim cudem
Muszę wykazać że 8[sqrt](3) - 5 /6 należy do przedziału 1/2;1 5/6
jest to związane z błędem względnym/bezwzględnym.
Nie wiem kompletnie jak do tego się zabrać.
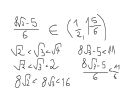
Dobra, kolega podpowiedział, ja tak na samym początku zrobiłem.
coś takiego zrobiłem
No to jeden kraniec przedziału masz udowodniony, teraz jeszcze drugi. sqrt(1)=1 i tym samym tokiem rozumowania wychodzi 1/2.
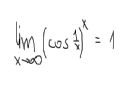
Czy ktos moze powiedziec, dlaczego tak jest?
Bo przeciez stosujac ten sam tok myslenia dojdziemy do wniosku, ze granica (1+1/x)^x gdy x dazy do nieskonczonosci wynosi 1, a nie e. Czyli: 1/x to musi byc rowne 0. A cosinus z 0 jest rowny 1. Stad tez 1 do potegi nieskonczonej daje 1, co dzialaloby tez we wspomnianym przykladzie.
Cosinus z prawie zera jest troche mniejszy od jedynki, a podnoszac cos troche mniejszego od jedynki do gigantycznej potegi otrzymamy prawie zero. Czyli granica powinna wynosic zero.
Podejrzewam blad w odpowiedziach, no ale zeby takie byki znajdowac w 10 wydaniu?
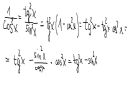
Sprawa druga:
Wiadomo ze pochodna tgx wynosi 1/(cosx)^2, czyli (tgx)^2 + 1
Zastanawia mnie jedno -> co tu jest zle? Od kiedy (tgx)^2 + 1 = (tgx)^2 - (sinx)^2?
edit: Moj mozg jest najwieksza zagadka tego wszechswiata. Ciekawe jakim cudem mnozac licznik i mianownik przez (sinx)^2 mialbym usunac (sinx)^2 z mianownika i dodac go do licznika. Ciekawe :)
W kazdym razie dzieki za pomoc.
A co do pierwszego problemu z granica ciagu, czy 0 to prawidlowa odpowiedz?
[81] (tgx)^2 + 1 = (tgx)^2 - (sinx)^2?
Od nigdy, bo to by znaczyło, że kwadrat jest równy -1, a to trochę nieprawda.
Nieprawdziwe jest przejście (tgx)^2 / (sinx)^2 = (tgx)^2 * (1-(cosx)^2), powinno być = (tgx)^2 / (1-(cosx)^2)
Mozna wiedziec, jak obliczyc kat alfa jesli wiem, ze tg alfa = 2 + sqrt(3)?
Korzystajac z funkcji cyklometrycznych. Wynik to 5*Pi/12 .
edit. [80]
Przy podstawieniu granica ta wynosi 1^niesk, dlatego trzeba wybrać inny sposób (limes opuszczam):
e ^ (ln(cos(1/x))^x) = e ^ (x * ln(cos(1/x))) =liczymy granicę tylko z potęgi= ln(cos(1/x)) / (1/x) =[0/0] więc korzystamy z l'Hospitala= -sin(1/x) / cos(1/x) = - tg(1/x) = 0, więc e^0 = 1
EDIT. O, sorry, zapomniałem o logarytmie. To typowy sposób rozwiązywania granicy, gdy wychodzi Ci symbol nieoznaczony 1 do nieskończoności.
"Mozna wiedziec, jak obliczyc kat alfa jesli wiem, ze tg alfa = 2 + sqrt(3)?"
Jedyne co przychodzi mi do głowy, to - wiedząc, że ma wyjść 5pi/12, czyli 75 stopni = 30 stopni + 45 stopni - skorzystać ze wzoru na tangens sumy dwóch kątów i jakoś to wyprowadzić. W drugą stronę jest łatwo.
Nie, nie. Chce po prostu poprzez przeksztalcenia otrzymac dokladna wartosc kata alfa, wiedzac, ze tg alfa = 2+sqrt(3). Jak to zrobic? W ksiazce w tajemniczy sposob wychodzi ładna odpowiedz 5*Pi/12.
Co do [80] : czyli granica jest rowna 0, tak? Przypominam: w odpowiedziach podano, ze 1 - co jest wg mnie bez sensu.
EDIT: Jeszcze jedna watpliwosc:
"e ^ (x * cos(1/x)) =liczymy granicę tylko z potęgi"
Skad w ogole pojawilo sie tu e? lim[ cos(1/x)^x] = lim lne^(cos(1/x)^x), a nie e^(cos(1/x)^x)
Po prostu nie ogarniam.
Krawędzie prostopadłościanu mają długości 3,4,12 cm. Oblicz dł przekątnej prostopadłościanu. Jak niby mam to zrobić? Żeby obliczyć to z pitagorasa musiałbym mieć podane, która przekątna jest która.
Krawędzie prostopadłościanu mają długości 3,4,12 cm. Oblicz dł przekątnej prostopadłościanu. Jak niby mam to zrobić? Żeby obliczyć to z pitagorasa musiałbym mieć podane, która przekątna jest która.
Zacznij od dużego i dokładnego rysunku prostopadłościanu, oznacz długości boków, narusyj przekątne ścian bocznych, narysuje przekątną prostopadłościanu.
Wszystkie przekątne prostopadłościanu sa tej samej długości :)
Licząc w pamięci:
przekątna ściany 3x4 to 5
dalej przekątna 5 i krawędź 12 i przekątna prostopadłościanu tworzą trójkąt prostokątny, i liczysz sam dalej :]
w ostrosłupie prawidłowym czworokątnym przekątna podstawy ma dł 26 cm. Widząc, że spodek wysokosci ostrosłupa znajduje się w odległosci 12 cm od krawędzi boccznej oblicz obj tego ostrosłupa
Czy w tym zadaniu nie ma błędu? Odległosc powinna byc chyba 13....
A i jeszcze 2 zadanie:
Podstawą ostrodłupa prostego jest trójkąt prostokątny o przyprostokątnych 6 i 8 cm. Wysokość ostrosłupa jest równa 12 cm. Oblicz pole powieszchni całk tego ostrosłupa.
Potrzebna mi jest do tego dł kraw bocznej. Niestety nie wiem jak ją obliczyć z podanych danych.
w ostrosłupie prawidłowym czworokątnym przekątna podstawy ma dł 26 cm. Widząc, że spodek wysokosci ostrosłupa znajduje się w odległosci 12 cm od krawędzi boccznej oblicz obj tego ostrosłupa
Czy w tym zadaniu nie ma błędu? Odległosc powinna byc chyba 13....
Odległość punktu A od prostej k mierzymy, rysując prostą l przecinającą prostą k pod kątem prosty i przechodzącą przez punkt A.

mam problem, pewnie wyda sie wam banalny, ale ja za nic nie moge wpasc na to jak to rozgryzc..
ogolnie rozchodzi sie o to, ze mam wyznaczyc dziedziny takich funkcji -->
wiem, ze w tym pierwszym trzeba miec takie oto rownanie - x^2 + 1 > 0
ale co po tym?
a na to drugie kompletnie nie mam pomyslu..
Dziedzina funkcji jest to przedział/zbiór iksów dla których wynik funkcji jest wymierny. Czyli w pierwszym przypadku zawsze gdy to co jest pod pierwiastkiem jest większe-równe 0 i to co w mianowniku jest różne od 0. A w drugim przypadku gdy to co w mianowniku jest różne od zera.
w drugim masz rzeczywiste
czyli w drugim przypadku dziedzina sa wszystkie liczby rzeczywiste?
a w pierwszym?
ale w rozwiazaniu wystarczy napisac x^2 > -1 i to wszystko?
w takim razie dziedzina nie bedzie - D=R/‹-1,1›? sam nie wiem
(-1)^2 = 1 > -1
(-0,1285)^2 > -1
itd.
Wniosek wyciągnij sam.
masz kwadrat a kwadrat nigdy nie jest ujemny wiec rowniez rzeczywiste
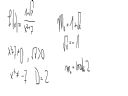
okej, to jeszcze sprawdzcie czy to mam dobrze -->
Jeśli będziesz się babrał w rozwiązywanie nierówności typu x^2+cokolwiek > 0 i będziesz to jakoś przekształcał, pierwiastkował, cudował, to życzę powodzenia na maturze czy klasówce... Podobnież z równaniem sqrt(x)+1=0. W takich przypadkach NA OKO widać, że nie ma rozwiązania albo dziedziną są rzeczywiste. Jeżeli nie widać, to znaczy, że mamy za mało praktyki w liczeniu i przekształceniach.
I co to w ogóle jest m_0? To ma coś wspólnego z "miejsce zerowe"? Jeśli tak, to zapis m_0 = 1+sqrt(x) jest bardzo niefortunny i w sumie nie wiem co wnosi :/
m0 - miejsce zerowe
w takim razie co wynika z takiego czegos - 5 + sqrt(x) = 0?
bo jak dla mnie tylko to, ze sqrt(x) = -5 ? w takim razie co z miejscem zerowym? mozecie mnie wysmiac, ale nie mam zadnego pomyslu na to..
Więc dla ułatwienia sobie życia zapamiętaj, że (przynajmniej dopóki jesteś na poziomie najwyżej szkoły średniej, a zakładam, że tak):
1. pierwiastek drugiego stopnia z czegokolwiek ZAWSZE będzie >= 0 (większy lub równy zero). Czyli równanie sqrt(cokolwiek) + innecokolwiek = 0 NIE MA ROZWIĄZAŃ (o ile tylko innecokolwiek jest dodatnie). sqrt() to zapis pierwiastka. Ponadto owo cokolwiek (pod pierwiastkiem) MUSI być >= 0 (i na tej podstawie wyznaczasz dziedzinę funkcji)
2. druga potęga (czyli "kwadrat") czegokolwiek ZAWSZE będzie >= 0 (większa lub równa zero). Czyli nierówność cokolwiek^2 + innecokolwiek > 0 (albo cokolwiek^2 + innecokolwiek >= 0) będzie ZAWSZE spełniona (czyli prawdziwa dla dowolnego cokolwiek) - oczywiście znowu po cichu zakładam, że innecokolwiek jest dodatnie (a w drugim przypadku - tym w nawiasie - przynajmniej nieujemne). Tutaj już nie mamy ograniczeń na to, jakie ma być cokolwiek - w przeciwieństwie do pierwszego punktu (gdzie musiało być nieujemne ze względu na to, że było pod pierwiastkiem) będąc podstawą potęgi może być jakiekolwiek (dodatnie, ujemne, zerowe)
Zastanów się nad powyższymi stwierdzeniami tak długo, aż dojdziesz do wniosku, że przecież to oczywiste.
Przekładając to na twoje problemy:
sqrt(x)+5=0 nie ma rozwiązań (bo sqrt(x)+5 ZAWSZE będzie >0), natomiast mamy warunek, że x>=0 (pomoże w obliczaniu dziedziny funkcji). Nie ma sensu przerzucać 5 na drugą stronę, bo to można zrobić w pamięci i dostajesz wtedy sqrt(x)=-5 a to OCZYWISTA sprzeczność.
x^2 + 7 ZAWSZE będzie >0, czyli w szczególności różny od 0. Zatem ponownie nie ma sensu rozmyślać nad nierównością x^2+7>0 ani nad tym czy x^2+7 jest różne od 0, bo to zawsze prawda.
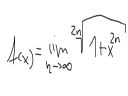
Taka funkcja:
To oczywiscie to samo co lim (1+x^2n)^1/(2n)
Czy moge zalozyc, ze 1 w porownaniu do x^2n jest tak male, ze pomijalne, i zapisac to jako (x^2n)^1/(2n)?
Wychodzi wtedy y=|x| i gdy |x|<1; y=1, tak?
(1+x^(2n))^(1/(2n)) - skoro pierwszy nawias dąży do nieskończoności a drugi do 0 to imho jest to wyrażenie nieoznaczone inf^(0)
gdzie inf to nieskończoność.
[103] Imo wystarczy zastosować sposób, który wykorzystałem w [85]. Pozbędziesz się wtedy potęgi i możesz skorzystać z l'Hospitala.
edit. Chociaż wg Wolframa ma wyjść tak jak mówisz, czyli: y=|x| i gdy |x|<1; y=1. Chociaż sam nie wiem dlaczego tak jest. :D
http://www.wolframalpha.com/input/?i=lim&a=*C.lim-_*Calculator.dflt-&f2=%281%2Bx%5E%282n%29%29%5E%281%2F2n%29&f=Limit.limitfunction_%281%2Bx%5E%282n%29%29%5E%281%2F2n%29&f3=n&f=Limit.limitvariable_n&f4=inf&f=Limit.limit_inf&a=*FVarOpt.1-_**-.***Limit.direction---.**Limit.limitvariable---
"Z miejscowości A do B jednoczesnie wyjechały dwie ciezarowki. Pierwsza polowe czasu przeznaczonego na przebycie drogi pokonala z V= 50km/h a druga polowe z V=40km/h. Druga ciezarowka polowe drogi jechala z V=40km/h a pozostala czesc z V=50km/h. Ktora z ciezarowek byla pierwsza w B?"
Chodzi mi o to jak zacząć. Wiem że jedna z tych wartości jest średnią harmoniczną.
Nauczyciel nic nie tłumaczy, proszę o pewne sprostowanie.
pre ==> Nie kombinuj ze średnimi (jedna z KTÓRYCH wartości jest średnią harmoniczną? gdzieś dzwoni ale nie wiadomo gdzie? ;) ), tylko rozwiąż to powoli, po kolei i po ludzku. Oznacz sobie połowę czasu przeznaczonego na przebycie drogi (przez pierwszą ciężarówkę) jako t i wylicz prędkość średnią. To samo z drugą ciężarówką - oznacz sobie połowę drogi przez s i wylicz prędkość średnią.
pajkul ==> Co to znaczy "jest pomijalnie małe w porównaniu do x^2n"? A jak x będzie z przedziału (0,1) to też 1 będzie pomijalnie małe? Tak do tego nie podchodź.
DEXiu - mam rozumieć że t= 1/2 czasu potrzebnego na objazd a 2t= to czas całkowity dla 1 ciężarówki.
Analogicznie tylko że dla s i dla drugiej cięzarówki?
dexiu -> Pomijalnie male gdy |x|>1, a rozpatrujac to dla |x|<1 wychodzi, ze f(x)=1, czyli tak jak ma byc.
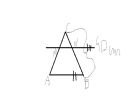
Potrzebują pomocy. Mam zadanie
W trójkącie ABC przeprowadzono prostą równoległą do boku AB, przecinająca bok AC w pkt M, a bok BC w pkt N. Oblicz długość odcinkó BN i NC, wiedząc, że |AM|/|MC| = 2|3 i |BC| = 40 cm.
Rysunek to będzie coś takiego... Ale co dalej? Próbowałem jakiś obliczeń ale nic mi nie wychodzi.
Proszę o pomoc...
pre ==> No chyba wyraźnie napisałem. W jednym przypadku zobaczysz, że prędkość średnia będzie średnią arytmetyczną, a w drugim - harmoniczną. I naprawdę szkoda sobie głowę zaprzątać pamiętaniem kiedy taka, a kiedy taka - to można zwyczajnie policzyć korzystając tylko i wyłącznie ze wzoru v=s/t (i przekształceń) oraz wiedząc, że prędkość średnia to droga całkowita przez czas całkowity. I zwróć uwagę, że dla pierwszej masz podane prędkości dla pierwszej i drugiej połowy CZASU, a dla drugiej ciężarówki - dla pierwszej i drugiej połowy DROGI.
Captain ==> W czym konkretnie problem? Twierdzenie Talesa znasz? Jak nie znasz albo nie pamiętasz, to z podobieństwa trójkątów też przejdzie.
Podpowiedź:
spoiler start
|BN|/|NC| = |AM|/|MC| = 2/3
spoiler stop
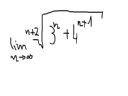
Do obliczenia granicy wykorzystac twierdzenie o 3 ciagach.
Jesli chodzi o odpowiedz, to raczej nie chce mi sie wierzyc ze wychodzi 1. Jak to w ogole ugryzc?
Wiesz jak się stosuje twierdzenie o trzech ciągach?
a(n) := 4^n
b(n) := (3^n + 4(n+1))
c(n) := (4^n + 4^(n+1)) = (1/4 * 4^(n+1) + 4^(n+1)) = 5/4 * 4^n
a(n) < b(n) < c(n) % porównaj zapis w pierwszej kolumnie
rt(n+2)(a(n)) <= rt(n+2)(b(n)) <= rt(n+2)(c(n)) % ponieważ wszystkie a(n), b(n) i c(n) są większe od 1
Z twierdzenia o trzech ciągach granica środkowego zachowuje te nierówności. Ale przecież:
lim rt(n+2)(a(n)) = lim rt(n+2)(4^n) = lim 4^(n/(n+2)) = 4
lim rt(n+2)(c(n)) = lim rt(n+2)(5/4 * 4^(n+1)) = lim rt(n+2)(5/4) * 4^((n+1)/(n+2)) = 4
więc:
4 <= lim rt(n+2)(b(n)) <= 4
lim rt(n+2)(b(n)) = 4
A tak na przyszłość: nie używasz żadnego podręcznika do analizy np. Fiftenholza czy Birkholza? Nie ma tam przykładów na zastosowanie twierdzeń?
LOL?
lim rt(n+2)(5/4) * 4^((n+1)/(n+2)) = 4 - granica tego podkreslonego to 4, a wiadomo, ze granica stałej to ta stała, wiec 5/4 * 4 = 5.
A od kiedy sqrt[n+2](5/4) jest stałą niezależną od n? (sorry, mam troszkę inne oznaczenia, ale to z przyzwyczajenia ;)
pajkul ~~~>
DEX Ci już odpowiedział, ale ja dojaśnię:
lim [rt[n+2](5/4) * 4^((n+1)/(n+2))]
To co doprowadziło do tego wyrażenia to rozdzielenie pierwiastka iloczynu. W wyrażeniu pod granicą (dodałem nawiasy kwadratowe, żeby jasno było widać czego to jest granica) jest iloczyn dwóch czynników zależnych od n.
Przy n -> +inf
rt[n+2](5/4) -> 1
4^((n+1)/(n+2)) -> 4
Prawda? A granica iloczynu dwóch ciągów, których granice istnieją, jest iloczynem granic.
Nie wierzysz? Sprawdź na Wolframie:
http://www.wolframalpha.com/input/?i=lim+%285%2F4+*+4%5E%28n%2B1%29%29%5E%281%2F%28n%2B2%29%29
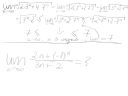
Mam tu jeszcze 1 przykład do sprawdzenia i chciałem zapytać jak zrobić drugi z wykorzystaniem twierdzenia o 3 ciągach.
ile to będzie?
(-6)+8:4
Chudy ~~~>
Pierwsze zadanie:
Można prościej. Zauważ, że:
4 * 7^n < 2 * 3^n + 4 * 7^n < 5 * 7^n
bo 2 * 3^n < 7^n
Dalej tak, jak w zadaniu pajkula.
lim rt[n](c * 7^n) = lim [rt[n](c) * 7]
a granica iloczynu dwóch ciągów, których granice istnieją, jest iloczynem granic. To załatwia oszacowanie zarówno górne jak i dolne przez liczbę 7.
Drugie zadanie:
Zauważ, że (-1)^n jest ciągiem ograniczonym (naprzemienne wyrazy -1 i 1). Zatem:
lim [(-1)^n] / n = 0
Czyli zastosowanie tej metody, którą stosowałeś dla granic f-cji wymiernych, też tu działa tak jak trzeba. Nie ma potrzeby stosowania tw. o trzech ciągach. Choć można. Fukcja ograniczająca od dołu będzie przyjmowała -1 zamiast (-1)^n, a ta od góry: 1 zamiast (-1)^n.
Wystarczająco jasno?
BTW. Odnośnie stylu opisanego w pierwszym poście. Jak można pisać
sqrt[n]() - pierwiastek n-tego stopnia
Skoro sqrt to skrót od square root czyli pierwiastek kwadratowy?
Serio? :o Nie zwróciłem na to uwagi. Ale i całe szczęście, że nie piszę o analizie :)
*****
To przy okazji zapodam temat do myślenia. Wszystkim, którzy męczą się z granicami i myślą sobie "po co to", może coś da obserwacja, że granica jest jednym z czterech fundamentów matematyki. Całej matematyki.
Sumy szeregów to granice ciągu sum częściowych.
Całki to granice sum szeregów.
Pochodna to granica ilorazu różnicowego funkcji.
Z kolei pochodna jest podstawą dla równań różniczkowych jednej i wielu zmiennych.
A gro całego zastosowania matematyki w naukach przyrodniczych to rachunek równań różniczkowych cząstkowych. Od modelowania aerodynamicznego kształtu samolotów do modeli przewidywania pogody. Od sterowania procesami chemicznymi do utrzymywania populacji wilków w rozsądnych granicach. Może kogoś to natchnie do myślenia, że to nie jest takie bez sensu ;)
Mipari ==> Masz iloczyn stałego współczynnika przez funkcję, która nie jest tożsamościowo równa 0. Aby zatem cały ten iloczyn był t. r. 0, to ten współczynnik musi być zerem.
(funkcja jest tożsamościowo równa 0, kiedy jest równa 0 dla każdego argumentu)
Orientuje się ktoś może jakiego wzoru używa się zazwyczaj do wyliczania klasycznego współczynnika asymetrii w statystyce na poziomie szkoły wyższej?
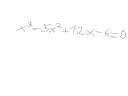
Potrzebna pomoc z wielomianów, mianowicie nie wiem jak znaleźć x w tym przykładzie:
@up
weneckie ~~~>
Ogólną definicję momentu pewnie znasz.
Trzeci moment to: mi_3 = E(X - EX)^3
Asymetria (spłaszczenie) to znormalizowany 3-ci moment, czyli:
alfa_3 = (E(X - EX)^3) / (D^2X)^(3/2)
EX - wartość oczekiwana (1-szy moment)
D^2X - wariancja (2-gi moment)
Co asymetria oznacza dla zmiennej losowej danego typu, to można samemu sobie policzyć lub sprawdzić w tabelach. Ale czasem łatwiej się liczy na podstawie innych własności zmiennej losowej.
http://textbook.statsoft.pl/stathome_stat.html?http%3A%2F%2Ftextbook.statsoft.pl%2Fstbasic.html
przeszukaj po skośności lub asymetrii
jakieś wyciągi z wzorów można znaleźć też tu:
http://www.ekonometria.4me.pl/statystyka2.htm
http://www.ekonometria.4me.pl/wzory.htm
http://pl.wikibooks.org/wiki/Statystyka_matematyczna/Momenty_statystyczne_ciągłe_i_dyskretne#wz.C3.B3r_3.9
Mam nadzieję, że się przyda.
Dzięki jiser, przyda się.
http://imageshack.us/photo/my-images/580/img20111210174004.jpg/
potrzebuje pomocy z zadaniem 2.201 (nie zwracajcie uwagi na przekreslenie, ma byc geometryczny ;))
dochodze do q^4=85/2 i to jest zarazem ostatni wyraz ciagu bn, ale co dalej?
[135]
Imo, jeśli a1=b1 i a5=b5 i oba te ciągi są geometryczne, to ciąg a = ciąg b. A co za tym idzie sumy ich pierwszych pięciu wyrazów są takie same - dlatego dla ciągu geometrycznego nie ma sensu to zadanie. Jeśli wziąć pod uwagę skreślenie to:
Wyliczasz w ciągu arytmetycznym na podstawie danych najpierw r, potem a5. Wiedząc, że a1=b1 i a5=b5, obliczasz q w ciągu geometrycznym (będą 2 możliwości) i z tego ostatecznie sumę pierwszych pięciu wyrazów.
edit.
spoiler start
a1+a2+a3+a4+a5 = 85/2
5*a1 + 10*r = 85/2 --> r = 15/4 = 3,75
a5 = a1+4r = 1+15 = 16
b5/b1 = 16/1 = (b1*q^4)/b1 = q^4 = 16 --> q = 2 v q = -2
b1+b2+b3+b4+b5 = ?
b1*(1+q+q^2+q^3+q^4) =
dla q=2: 1+2+4+8+16 = 31
dla q=2: 1-2+4-8+16 = 11
spoiler stop
aha, wlasnie tak myslalem, dzieki
jak bede mial problem z wyliczeniem (choc nie powinien sie pojawic) to poinformuje
a teraz wspanialych derbow zycze :D
a jak to r wyliczyc?
EDIT
juz mam, r wychodzi 4 i 1/4
wyraz 5 =17
r=4 i 1/4
i q probuje wyliczyc ze wzoru ogolnego no ale mi wychodzi q^4=17
nie wiem jak sie za to zabrac....
EDIT
dobra, juz przepraszam za klopot, zrobilem
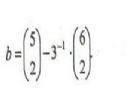
Może głupie pytanie, ale ile powinna wyjść liczba b? Zaskoczył mnie trochę ten zapis i w sumie jestem w lekkim szoku, bo niby to jest proste, ale nie wiem, jak się za to zabrać.
Wyszło mi 50, ale coś pokręciłem chyba. Można prosić o jakąś pomoc?
NeroTFP.-->który zapis wprawia cię w zakłopotanie?
tu masz wzór na rozpisanie symbolu Newtona: http://pl.wikipedia.org/wiki/Symbol_Newtona
a ułamek 3^-1 to to samo co (1/3)^1
Mi wyszło b=2,5
Właśnie żaden nie wprawiał, bo umiałem to rozpisać. Problem tkwił w tym, że zamiast -3, zapisałem sobie *3 i zamiast odejmować, to w konsekwencji mnożyłem. Tak to jest, jak się źle przepisze.
Ps: Nie wiem, czy ja zrobiłem błąd, ale przeliczyłem dwa razy i b wyszło mi 5. Ale pewnie gdzieś się pomyliłem.
Chyba Łysy. się gdzieś walnął w obliczeniach bo mi również wyszło 5.
Pytanko
Funkcja kwadratowa, w której ax^2+bx+c gdzie a,b, c są dodatnia nie przecina wykresu funkcji, a gdy wszystkie są ujemne to też prawda?? Czy dotyczy to także wiekszych wielomianów?
trelabela ==> Napisz to jeszcze raz - tym razem po polsku i składnie, używając poprawnych pojęć matematycznych. Tego co napisałeś zrozumieć się nie da.
Gdy mamy do czynienia z funkcją kwadratową o wzorze ogólnym ax^2+bx+c gdzie a,b, c są dodatnie, to funkcja ta nie przecina osi x? Czy dzieje się tak również w tedy gdy a,b,c są ujemne?
Pomyśl chwilę. Przecież to to samo pytanie tak naprawdę.
Jeśli a, b, c < 0 to -a, -b, -c > 0
więc -(ax^2 + bx +c) jest zawsze dodatnie.
A nieprzecinanie osi x to z perspektywy algebraicznej stwierdzenie, że suma jest ciągle tego samego znaku. Skupmy się na stronie dodatniej.
ax^2 + c jest zawsze dodatnie. Trzeba tłumaczyć?
Ale bx już nie. Ba, łatwo sobie skonstruować przykład, że tak nie jest. Przyjmijmy, że pewna parabola (o a=1) jednak przecina oś x w wartościach n i m. Czy da się osiągnąć dodatnie b?
(x - n)(x - m) = x^2 - 2(n+m)x + nm
Czyli nm musi być dodatnie, ale (n + m) nie. -1 i -2 wyglądają na dobre.
(x + 1)(x + 2) = x^2 + 3x + 2
Działa? Dodatnie? Ale przecina?
Warunek, który Cię interesuje, to ujemność delty. Ją też można wyprowadzić. Ale bez przesady. Myślenie i czytanie nie boli ;p Jest na wiki.
Nie. Nie można wysnuć takiego wniosku. Wystarczy, że dla dodatnich a,b,c będzie zachodziła nierówność b^2 > 4ac - wówczas funkcja będzie przecinała oś OX. Analogicznie dla przypadku ujemnych a,b,c. Jeżeli przez "większe wielomiany" rozumiesz wielomiany wyższych stopni, to również nie da się wysnuć takiego wniosku ogólnego. Co więcej - wielomiany stopni nieparzystych ZAWSZE będą co najmniej raz przecinać oś OX.
Mam problem, nie pamiętam jak się robi równania wielomianowe ;<
Mam do policzenia takie równanie:
t^4-2t^3-2t^2+6t-3=0
Jakby ktoś podał mi metodę rozwiązania, to byłbym wdzięczny ^^
Majezon ~~>
Twierdzenie Bezouta i dzielenie wielomianów.
Albo metoda odgadywania - przekształcanie do takiej postaci "że widać".
W pamięci znalazłem już jeden.
Tu masz zastosowanie z przykładem
http://matematyka.pisz.pl/strona/121.html
To jeden to i ja znalazłem :P
Z odpowiedzi do zadania wnioskuję, że innymi pierwiastkami są pierwiastek z 3 i minus pierwiastek z 3. Zaraz postaram się zrobić z tego Bezouta. Dzięki za pomoc :)
Majezon ==> Tylko że tak "normalnie" raczej nie będziesz miał dostępu do odpowiedzi. I mylisz się, że znalazłeś "na oko" tylko jeden pierwiastek, bo tak naprawdę znalazłeś dwa. 1 jest tutaj pierwiastkiem podwójnym i gdybyś to odkrył, to zostałoby Ci do rozwiązania trywialne równanie kwadratowe t^2-3=0 skąd dostałbyś te +/- sqrt(3)
[152] Faktycznie, jak podzieliłem przez (x-1) to wyszło, że 1 jest podwójnym pierwiastkiem. Myślałem, że da się to policzyć szybciej(i pewnie się da), ale muszę nad tym popracować trochę ^^
Jeszcze raz dzięki za pomoc i odpowiedź :)
"Myślałem, że da się to policzyć szybciej(i pewnie się da)"
Da się bardzo prosto, tylko że ciężko to komuś wytłumaczyć - musisz na to raczej sam wpaść. Ale spróbujmy. ;)
Gdy masz swoje równanie: t^4-2t^3-2t^2+6t-3=0 i wiesz, że pierwiastkiem jest t=1, to zapisujesz to (t-1), przez które byś dzielił ten wielomian i ustalasz taki wielomian stopnia o 1-mniejszy, że po pomnożeniu go przez Twój znaleziony już pierwiastek da Ci wielomian, od którego zacząłeś. Czyli coś takiego: (t - 1)(t^3 - t^2 - 3t + 3). No i w drugim nawiasie otrzymuję to, co otrzymałbym po podzieleniu głównego wielomianu przez znaleziony pierwiastek, ale 5 razy szybciej. Napierw daję t^3, bo muszę mieć t^4, a po pomnożeniu przez t da mi to właśnie t^4, ale mam też -1, przez którą muszę pomnożyć, więc dostaję jakby w pamięci t^4-t^3, czyli t^4 jest w porządku, ale mam mieć jeszcze -2t^3, więc muszę dać -t^2, bo to z kolei gdy pomnożę przez t, da mi -t^3, a -t^3 i -t^3 daje -2t^3, które chcę mieć, itd. itp. Ciężko to brzmi, ale jak wpadniesz na to, jak to robić, to takie zdanie robisz w minutę. :)
Mam 2 zadania. Moglibyście sprawdzić czy mam dobre wyniki?
1 - Ile licz trzycyfrowych można utworzyc z cyfr ze zbioru : 1,2,3,4,5,6,7 jeśli cyfry w liczbie mogą się powtarzać,oraz : a) wystąpi cyfra 2 b) liczba ma być parzysta c) wystąpi cyfra 3 i nie wystąpi cyfra 7
2 - Na ile sposobów na ławce może usiąść 11 graczów piłki nożnej jeśli : a) usadzimy ich losowo b) bramkarz usiądzie jako pierwszy c) bramkarz i środkowy napastnik nie usiądą obok siebie
Moje wyniki:
1
a)49
b) 196
c)36
2
a)39916800
b)3628800
c) Nie umiem tego zrobić i proszę o pomoc :P
[157]
To e nigdzie nie zniknęło, tylko gdy mamy taką granicę, można to liczyć tylko z potęgi i potem wynik podstawić do tego e. Czyli np. granica potęgi (tego po prawej stronie) wychodzi 2, to ostatecznym wynikiem jest e^2. Nie sądzę, żeby znak równa się = był tam prawidłowo postawiony.
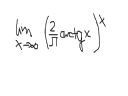
Chodzi o to, ze jest do rozwiazania taki przyklad z de'l'hospitala i nie wiem jak go rozwiazac. Analizujac rozwiazanie znalazlem taki fragment i nie wiem skad sie on wzial. Bo to, co dzieje sie pozniej jest oczywiste i zrozumiale dla mnie, latwo zastosowac hospitala, ale przejscie z lewej strony "=" do prawej jest dla mnie niezrozumiale. Nie mowie ze to rozwiazanie z jakiejs ksiazki, ale pewnie przez studenta.
Przyklad o ktory sie rozchodzi ->
jagged_alliahdnbedffds -> Dobra, juz rozumiem o co chodzilo i jak sobie z tym poradzic.
mam do zrobienia jedno rwonanie z ktorym mam problemik z funkcji potegowej
1. sqrt(x^2+7) -x=2
i tu wychodzi mi x=3/4 a w odpowiedziach mam 2, kompletnie nie wiem dlaczego, sprawdzalem 2 razy i nic, ciagle to samo
jest ok, blad w odpowiedziach, sprawdzalem kilka razy, ale chcialem sie upewnic, dzieki :)
mam jeszcze jeden przyklad z watpliwosciami
sqrt(7+sqrt(x))=1+ sqrt(x)
no i tutaj wychodza dwa rozwiazania mianowicie 9 i 4, u mnie wychodzi ze poprawne jest 9 a w odpowiedziach jest 4, a nie wiem skad bo dziedzine wyznaczylem chyba dobra (rzeczywiste dodatnie z zerem) no i zastrzezenie x>6, wiec bylbym wdzieczny o sprawdzenie
ekhm a znasz jakis pierwiastek ktory jest rowny -3 ??/Wiec jakim prawem go podnosisz do kwadratu????????????????????????????????????????????????
I czemu x>6??
sqrtx > - 7 co jest spelnione dla R.
mialem wszystko ok, tylko zastrz. zle policzylem (glupi blad) i wyszlo ze mniejsze od 6, ale dzieki za pomoc :)
co prawda nie wiem za bardzo o co Ci chodzi ale napisze jak robilem
dziedzina
podnioslem do kwadratu zatem zlikwidowalem duzy pierwiastek
tutaj musi sie pojawic zastrzezenie zebym mogl zkwadratowac wiec x mniejsze lub rowne 6
no i potem z rownania kwadratowego
ja sie pomylilem przy zastrzezeniu, zle zmienilem znak
sqrt(7 + sqrt(x)) = 1 + sqrt(x)
D: x>=0
Podnoszę do kwadratu (nie piszę wartości bezwzględnych, bo dziedzina jaką mamy pozwala nam na zapisanie tego od razu tak):
7 + sqrt(x) = 1 + 2*sqrt(2) + x
x + sqrt(x) - 6 = 0
sqrt(x) = t
t^2 + t - 6 = 0
(t - 2)(t+3) = 0
t = 2 lub t = -3
sqrt(x) = 2 --> x = 4
Szybkie pytanie.
Czy korzystając ze schematu Hornera da się podzielić wielomian przez dwumian w którym współczynnik a1 jest różny od 1? na przykład (-2x+1)?
"Przy dzieleniu wielomianów schemat Hornera można stosować tylko wtedy gdy w dwumianie nie ma przy żadnej potęgi i współczynnika."
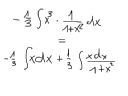
Mozna wiedziec, dlaczego to jest rowne? Naprawde nie potrafie tego zrozumiec.
edit: No jasne, funkcja wymierna x^3/(1+x^2) zamieniona zostala na x - [x/(x^2+1)].
Hej, jakim sposobem rozwiązywać nierówności takie jak np ta?
3x^2 + 5x +7 jest większe lub równe 0 ?
W równaniu normalnie wyliczyłbym delte itd ale jak to jest w przypadku nierówności?
Też liczysz deltę. Potem z wykresu przecież widzisz gdzie jest większe a gdzie mniejsze od zera.
Garret Rendellson - http://matematyka.pisz.pl/strona/93.html
http://www.bazywiedzy.com/nierownosci-kwadratowe.php
Wynikiem takiej nierówności są po prostu przedziały x w których funkcja ma wartości większe lub mniejsze od zera.
A co jak wyjdzie ujemna delta? Wtedy wynik należy do zbioru nieskończonego tak? W przypadku równania 3x^2 +5x +7
ps przepraszam za 2 posty pod rząd ale coś się z editem zepsuło
To gdzie będzie leżał wierzchołek paraboli zależy od współczynnika a (tego samego, którego używasz do liczenia delty) oraz wartości pierwiastków.
I
Dwa pierwiastki + dodatnie a -> ramiona paraboli skierowane w górę i wierzchołek pod osią OX, zbiorem rozwiązań jest zakres, którego granicami są pierwiastki
II
Dwa pierwiastki + ujemne a -> ramiona paraboli skierowane w dół i wierzchołek nad osią OX, zbiorem rozwiązań jest zakres, którego granicami są pierwiastki
III
Jeden pierwiastek (delta = 0) + dodatnie a -> ramiona paraboli skierowane w górę i wierzchołek na osi OX, z rozwiązaniami trzeba pokombinować, wierzchołek leży na OX więc musisz zwrócić uwagę na to, czy jest to nierówność mocna czy słaba, żeby stwierdzić, czy pierwiastek też ma należeć do zbioru rozwiazań
IV
Jeden pierwiastek (delta = 0) + ujemne a -> ramiona paraboli skierowane w górę i wierzchołek na osi OX, rozwiązania - jak w punkcie wyżej
V
Nie ma pierwiastków (ujemna delta) + dodatnie a -> cały wykres znajduje się nad osią OX, oczywiście ramiona skierowane w górę, rozwiązaniem są albo wszystkie x albo nie ma rozwiązań, w zależności od tego, czy wartości mają być większe czy mniejsze od 0
VI
Nie ma pierwiastków (ujemna delta) + ujemne a -> cały wykres znajduje się pod osią OX, oczywiście ramiona skierowane w dół, rozwiązaniem są albo wszystkie x albo nie ma rozwiązań, w zależności od tego, czy wartości mają być większe czy mniejsze od 0
Robię to i robię i natrafiłem na takie zadanko:
jesli wiek piotra sprzed dziesięciu lat pomnożymy przez jego wiek za siedem lat przez jego wiek za siedem lat to otrzymamy liczbe nie większą od 60. Jeżeli natomisat jego wiek pomnożymy przez wiek sprzed roku to otrzymamy liczbę większą niż 132. Ile lat ma Piotr?
Robię to tak:
Z 1 równania wychodzi mi x^2 -3x -70 < lub równe 60
Delta = 289
x1 = -7
x2 = 10
2 równanie to x * (x-1) > 132
I teraz nie wiem co dalej. Myslałem, by podstawić tą 10 (lub -7 ale wiek nie może być ujemny) do tej drugiej nierówności. Ale wtedy wychodzi równanie sprzeczne.
W pierwszej nierówności delta nie wynosi 289 tylko 529, zapomniałeś przenieść 60 na drugą stronę.
Potem liczysz miejsca zerowe i bierzesz taki przedział, żeby nierówność była spełniona. (x1=-10; x2=13). To samo robisz z drugą nierównością. Jak masz już oba przedziały to bierzesz ich część wspólną xE<-10,11)u(12,13>
Aby drugi warunek zadania był spełniony ( 12*11=132, a więc nie jest to liczba większa, musi to być zatem 13, bo 13*12=156) , Piotr musi mieć 13 lat.
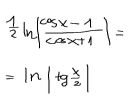
Czy mozna wiedziec, jak to przeksztalcono, ze otrzymano to co na dole?
No ludzie, przeciez umiem samodzielnie szukac wzorow. Wiem, ze tg(x/2)=(1-cosx)/sinx.
Gdyby znalezienie wzoru bylo problemem, nie pytalbym tutaj.
Nie wiem jak to zostalo przeksztalcone i nie bede sie z tym ukrywal.
Gotowy wzór na tangens kąta połówkowego (znajdziesz w każdych lepszych tablicach). Naprawdę chcesz wyprowadzenie? (sugerowana odpowiedź: nie ;)
moglby mi ktos przypomniec jak sie rozwiazuje nierownosci typu
x^-1 >1
x^-2<16
x^-2>x^-3
z gory dzieki
nie byłoby najlepiej po prostu odwrócić obie strony jednocześnie przekręcając znak nierówności?
edit: chociaz nie, to działa tylko przy parzystych potęgach.
jak odwrocic? przeciez tu sa potegi
nie wiem wlasnie jak dlatego prosze o wyjasnienie
Chyba najlepiej by było pomnożyć przez jakąś parzystą potęgę jednocześnie zakładając, że x =/= 0
w pierwszym mnożysz przez x^2
w drugim mnożysz przez x^2
w trzecim mnożysz przez x^4
Mam nadzieje że łapiesz schemat i dalej będzie łatwo.
Na przykładzie pierwszego:
x^(-1)>1
(1/x)-1>0
[1-(x^2)]/x>0
[1-(x^2)]*x>0
x=1 v x=(-1) x=0
Teraz na osi rysujesz przedziały (-inf;-1) u (1;+inf) i (0;+inf) i wyciągasz z tego część wspólną.
\/ ---Tak, sprawdzasz czy należy do dziedziny jeszcze :)
dzieki chlopaki
a dziedzina ma sie rozumiec ze jesli nie ma ulamkow lub pierwiastkow rzeczywiste?
Macco
no robie rysunek na podstaiw wielomianu, mam te trzy przedzialy i czesc wspolna z tych trzech jeszcze sprawdzam z dziedzina?
Mam zadanie takiej treści
Samolot zbliżający się do lotniska leci na wysokości 2400m. By wylądować musi schodzić pod kątem 4 stopni. Jak daleko od początku pasa startowego powinien zacząć ten manewr
Policzyłem i wyszło 167,76m, ale sprawdziłem w odpowiedziach i jest napisane, że prawidłowy wynik to 34,3km. Kompletnie nie wiem, co mogłem źle zrobić. Może ktoś sprawdzić, czy dobrze policzyłem, a jeśli nie to, co zrobiłem źle
$erek47 ==> A zastanowiłeś się choć przez sekundę, że Twoja odpowiedź w połączeniu z danymi z zadania oznaczałaby, że ten samolot musiałby pikować niemal pionowo w dół? (2,4 km różnicy wysokości do pokonania na odcinku nieco ponad 150 m? ;) ) Zrób jeszcze raz porządny rysunek (trójkąt prostokątny), zaznacz co wiesz i policz co należy.
Macco
nie wiem tylko dlaczego mam z tego zrobic czesc wspolna a nie zsumowac? w ogole nie mam pomyslu
EDIT
juz doszedlem, pomyliles sie chyba przy sprowadzaniu do wspolnego mianownika bo powinien wyjsc wielomian stopnia drugiego :) juz mam dobrze
Wszystko byłoby dobrze, gdyby nie jedno niedopatrzenie, ale mam prawidłowy wynik. W każdym razie dzięki za pomoc.
Witam.
Czy mógłby mi ktoś pomóc w rozwiązaniu równania? Trzeba to doprowadzić do równania kwadratowego i wyliczyć iksy przez deltę. Przynajmniej powiedzieć jak zacząć, bo nie mam pomysłu.
sqrt(3x+4) + sqrt(x-4) = 2*sqrt(x)
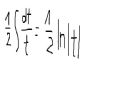
Mógłby mi ktoś wytłumaczyć jeden krok tego rozwiązania?
http://matematyka.pisz.pl/strona/2129.html
A dokładnie mówiąc ten ->
Chodzi o to że nie wiem skąd się wzięło to po prawej stronie. Z tego co wiem to dx/x to faktycznie ln|X| z tym że dt=2xdx, czyli pomimo tego dx mamy teź 2x więc na moje to powinno być
1/2*ln|x^2+1| +całka z 2x
Ktoś wie dlaczego tak?
dobra już wiem, zajechałem się.
pomoże ktoś o to zadanie
dla jakich wartości parametru m równanie 2^x+2^(x-1) 2^(x-2)+...=2^(2x-1) ma dwa różne rozwiązania