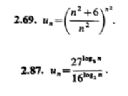
Analiza matematyczna - granice ciągów
Halo, w związku ze zbliżającym się sobotnim kołem z analizy ... wypadałoby się pouczyć. Czy mógłbym poprosić kogoś ambitnego i ociekającego chęcią pomocy o zrobienie dwóch przykładów ze zdjęcia po prawej? Zadań jest sporo więcej ale chciałbym zobaczyć jakiś gotowy, rozwiązany przykład ... abym mógł resztę oprzeć na tym 'schemacie'.
Polecenie: "znajdź granicę ciągu o wyrazie ogólnym'
Z góry dzięki.
____________
Jakbym je dodał to by weszło. :D
zakładam że granice dla n->oo.
lim(n->oo)((n^2+6)/n^2)^(n^2)= lim(n->oo)(1 +6/n^2)^(n^2)=1
wyjaśnienie 6/n^2 ->0, 1^(n^2)->1 , przy n->oo
W kolejnym nie widze podstawy logarytmu w liczniku. Możesz napisać co tam jest?
w liczniku podstawa to 3
w mianowniku podstawa to 2
Przynajmniej tak mi się wydaję bo sam nie mam tego w lepszej jakości. Dzięki za pierwsze, wszystko jasne ... i z góry dzięki za drugie. ;)

lo0ol --> Granica w pierwszym przykładzie to e^6. Granica drugiego to 0. Pierwszy masz na obrazku, drugiego na razie nie wiem, jak udowodnić, ale od razu można czuć, ze mianownik rośnie o wiele szybciej od licznika.
Z tego, co widzę, to przykłady masz z Analizy matematycznej Krysickiego i Włodarskiego, tam na końcu są odpowiedzi, które mogą Cię przynajmniej trochę naprowadzić. A jeśli chodzi o "naprowadzenie rozwiązaniami", to w samym Krysickim jest sporo przykładów rozwiązanych. Do tego polecam Bibliotekę Opracowań Matematycznych.
W drugim chodzi o wzory logarytmiczne
27^log(3)n= (3^3)^log(3)n= 3^3*log(3)n= 3^log(3)n^3=n^3
16^log(2)n=2^4*log(2)n=2^log(2)n^4=n^4
lim(n->oo)(n^3/n^4)=lim(n->oo)(1/n)=0
Co do pierwszego to oczywiście, mea culpa, minęło już pare lat od kiedy liczyłem takie rzeczy :)
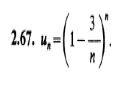
Nom około 25 zadań udało mi się zrobić ale mam problem jeszcze z dwoma. Jedno z nich <po prawej>. Mi wychodzi e^-3 ... a w odpowiedziach jest e^-(1/3). Mógłby ktoś pomóc?
(1 - 3/n)^n = (1 + (-3)/n)^n = e^(-3 * 1) = e^(-3) = 1/e^3 ?
W tym przypadku wszystko wskazuje na to, że w odpowiedziach jest drobny błąd. Wynikiem jest raczej e^(-3).
http://www.wolframalpha.com/input/?i=lim+n--%3E+inf+%281-3%2Fn%29%5En
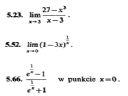
Granice funkcji
W związku z tym, że udało mi się załapać granice ciągów na zadowalającym dla mnie poziomie odnosząc to do sobotniego koła ... mam jeszcze granicę funkcji. No i prośba o zrobienie trzech zadań różnego typu, abym na waszych rozwiązaniach mógł oprzeć robienie następnych. Jeżeli ktoś znajdzie czas to dzięki.
5.23 Możesz zrobić na dwa sposoby.
1. Wyłączyć z licznika czynnik (x-3), który się "skróci" z mianownikiem.
27-x^3 = -(x-3)(x^2+3x+9)
Jak już Ci się "skróci", to masz granicę normalnego wielomianu, określonego w punkcie x=3, więc po prostu podstawiasz i wychodzi -(3^2+3*3+9)=-27
2. Jako że mamy do czynienia z wyrażeniem [0/0], możemy skorzystać z reguły de l'Hospitala, a więc policzyć pochodne licznika i mianownika (granica po takim manewrze się nie zmieni)
(27-x^3)'=-3x^2
(x-3)'=1
Zostaje nam zatem granica przy x-->3 z (-3x^2), podstawiamy 3 i ponownie wychodzi nam -27.
2. Ciekawą metodę pokazuje Wolfram jak naciśniesz "show steps", polecam.
http://www.wolframalpha.com/input/?i=lim+x+--%3E+0+%281-3x%29%5E%281%2Fx%29
3. Tutaj podstawiając sobie 0 do wzoru możemy czuć, że granice lewostronna i prawostronna będą różne. Policzmy więc je oddzielnie.
a) granica przy x --> 0-
1/x dąży wtedy do -inf, a zatem e^(1/x) dąży do 0
całe wyrażenie dąży więc do [(0-1)/(0+1)], czyli do -1
b) granica przy x--> 0+
1/x dąży wtedy do +inf, a zatem e^(1/x) dąży do nieskończoności
mamy zatem do czynienia z wyrażeniem [inf/inf], korzystamy z reguły de l'Hospitala
(e^(1/x)-1)'=-1/x^2 * e^(1/x)
(e^(1/x)+1)'=-1/x^2 * e^(1/x)
Obie pochodne są takie same, tak więc wszystko się zredukuje i granica wychodzi 1.