
Wątek ten poświęcony jest przede wszystkim wspólnej pomocy w rozwiązywaniu zadań matematycznych.
-------------------------------------------------------------------------------------------------------------
Regulamin:
- Piszemy tutaj tylko i wyłącznie zadania matematyczne (czyt. nie zbaczamy na na tematykę innych przedmiotów itd.) oraz odpowiedzi na konkretne np. równanie.
- W swych wypowiedziach zważamy na wszelkie znaki interpunkcyjne oraz ogólną logikę zdań.
- Wypowiadając się nie używamy wulgaryzmów oraz obraźliwych zwrotów w stosunku do innych użytkowników forum.
-------------------------------------------------------------------------------------------------------------
Polecana NOTACJA matematyczna:
Podstawowe symbole
+ - dodawanie
- - odejmowanie
* - mnożenie
/ lub ewentualnie : - dzielenie
^ - potęgowanie
Przykład: 3^(x-2)
sqrt() - pierwiastek kwadratowy (drugiego stopnia)
Przykład: 2+sqrt(3)
sqrt[n]() - pierwiastek n-tego stopnia
Przykład: 5-2*sqrt[3](7) ("pięć minus dwa pierwiastki sześcienne (pierwiastki trzeciego stopnia) z siedmiu")
[] () - nawiasy w kolejności od najbardziej zewnętrznych. Polecamy jednak używać tylko nawiasów okrągłych () - również zagnieżdżając jedne w drugie - gdyż nie powoduje to niejednoznaczności, a nawiasy kwadratowe [] mogą także oznaczać część całkowitą liczby.
UWAGA! Pilnuj, aby każdy otwarty nawias miał swoje zamknięcie! W przeciwnym razie wyrażenie jest praktycznie nie do odczytania!
Przykład: 1/(1+1/(1+1/(1+1/(...))))
inf - symbol nieskończoności
Litery greckie i inne symbole specjalne można zapisywać słownie lub dowolnym znakiem pod warunkiem opisania co on oznacza!
Ułamki zwykłe
Należy używać nawiasów aby licznik i mianownik były jednoznaczne.
Przykład: (3+7x)/(2y-5)
Przykład: 3+7x/(2y-5)
Przykład: 3+7x/2y-5
Powyższe przykłady NIE SĄ tożsame!
Ułamki piętrowe
Tu również należy używać nawiasów.
Przykład: (3+7x)/(2y-5/(17+2*z))
Liczby mieszane
Dla jednoznaczności liczby mieszane typu 3 1/2 ("trzy i jedna druga") należy zapisywać jako sumę, np. (3+1/2) - często będzie konieczne ujęcie jej w nawias - lub ułamek niewłaściwy, np. 7/2. Preferowany jest jednak zapis w postaci ułamka dziesiętnego (tam gdzie to możliwe, tzn. gdy ułamek taki nie będzie miał nieskończonego rozwinięcia dziesiętnego)
Przykład: (3+1/2)
Przykład: 7/2
Przykład: 3,5
-----------------------------------
Powyższa notacja jest wzorowana na składni LaTeXa. Nie polecamy jednak stosowania tej składni w pełnej wersji - forum GOL nie obsługuje markerów TeXa i nie przetwarza formuł, które z kolei są trudne do czytania przez ludzi.
-------------------------------------------------------------------------------------------------------------
Przydatne linki przy rozwiązywaniu zadań:
- http://www.matmana6.pl/
- http://www.poolicz.pl/
- http://www.obliczone.pl/
- http://www.wolframalpha.com/
- http://matematyka.pisz.pl/
-------------------------------------------------------------------------------------------------------------
Nowa część wątku zostanie utworzona po przekroczeniu 200 postów.
-------------------------------------------------------------------------------------------------------------
GOL-owi matematycy:
- lajtowy ziomek:) | Ogólnie: zakres wiedzy obejmujący materiał do klasy 3 Liceum. Chętnie pomogę z funkcji kwadratowej oraz wszelkich równań, nierówności. Słabość - Geometria. :P
- Filevandrel | Cały materiał LO i materiał z 2 lat studiowania elektroniki, łapać na maila [email protected] zawsze chętnie odpiszę!:)
- tomazzi | podstawówka, gimnazjum, liceum, co nie co ze studiów. Lubię zadania na rozkminkę :P
- DEXiu | cały zakres do szkoły średniej włącznie; matematyka "wyższa" na poziomie studenta uczelni technicznej (nie matematyki na uniwerku:) - mat. dyskretna, geometria, analiza, algebra, statystyka, probabilistyka; bardzo chętnie zadania i zagadki logiczne
- Maco | Zakres do LO i troszkę matematyki wyższej | Pięta achillesowa - trygonometria
- $ebs Master | Zakres - liceum, studia bez prawdopodobienstwa
- Łysy. | Cała rozkminka aż do liceum, szczególnie lubię geometrię. Potem analiza, algebra, podstawy dyskretnej, podstawy probabilistyki.
- Mathmi Thenthur | matematyka na poziomie szkoły średniej plus studia ekonomiczne: analiza, algebra, statystyka, rachunek prawdopodobieństwa; wybitnie nie lubię geometrii
- jagged | Zakres szkoły średniej + semestr informatyki na EAIiE (AGH) + wciąż studia informatyczne na Politechnice
-------------------------------------------------------------------------------------------------------------
Linki do bannerów:
- http://img685.imageshack.us/img685/9937/bannermatematyka.jpg ~by A's
- http://img232.imageshack.us/img232/9959/bannerme.png ~by lajtowy ziomek
- http://img842.imageshack.us/f/matma2j.jpg/ ~by A's
-------------------------------------------------------------------------------------------------------------
Poprzednia część:
- https://www.gry-online.pl/S043.asp?ID=10935595&N=1
Jutro idę zaliczyć Funkcje. Nie kocham ich, ale zaliczyć trzeba..

6 zadań, z którymi mam problemy, bardzo prosiłbym o pomoc - to te zaznaczone. Gdybyście mogli rozwiązania na kartce i ze skanem, bo to bawienie się w znaczki ^ nawiasy etc, troszke trwa :)
Z góry dzięki za pomoc
@Up--->
Usuń niewymierność z mianownika:
1/(sqrt(5) + sqrt(3)) + 1 * (sqrt(5) - sqrt(3))/(sqrt(5) - sqrt(3))= sqrt(5) - sqrt(3)/5-3+1= sqrt(5) - sqrt(3)/3
Szybkie, proste pytanie:
3sqrt(3) * 3sqrt(3) =
(Nie wiem czy dobrze napisałem, chodzi mi o Trzy pierwiastki z trzech, drugiego stopnia.)
Edit: Jednak, chyba źle
^
!edit! 3sqrt(3) * 3sqrt(3) = 27
:: [3] ::
1. Zaznaczam na pojedynczej osi X miejsca zerowe tej nierówności, rysuję szkic wykresu (współczynnik przy największej potędze x jest ujemny, więc zaczynam od dołu) i odczytuję odpowiedź: A=‹-2,-1,0,2,3›. Albo zauważam, że kwadrat jest zawsze większy od 0, więc go pomijam - tylko nie można zapomnieć o x=1!!!
2. b) Korzystam ze wzoru a^3-b^3=(a-b)(a^2+ab+b^2). W tym wypadku a=sqrt[3](2), b=4. Wymnażam, upraszczam i otrzymuję: (2+4*sqrt[3](4)+16*sqrt[3](2))/-62
7. Rozpisuję symbol Newton'a i znajduję n: n!/(2!*(n-2)!)=66 ... n^2-n-132=0 ... n=12
8. Korzystam ze wzoru: a^2-b^2=(a+b)(a-b). W tym wypadku a=sqrt(5)+sqrt(3), b=1. Muszę wykonać tę czynność dwukrotnie, zmieniając oczywiście a i b. Wymnażam, upraszczam i otrzymuję:
(sqrt(5)-3*sqrt(3)+2*sqrt(5)-7)/-11
1. Z twierdzeniami jest tak, że więcej tutaj lania wody i opowiadania, niż samego zapisu :P A tak naprawdę, to nie wiem jak to udowodnić ;)
5. Wymnażam mianownik i otrzymuję: 1/(10*sqrt(2)-10), z czego usuwam niewymierność z mianownika i mam odpowiedź (u=v=1/10): 1/10+1/10*sqrt(2)
Mam problem - jak narysować przekrój graniastosłupa trójkątnego (prostego), jeśli przechodzi on przez krawędź podstawy, przecina przeciwległą krawędź bocznąi jest nachylona do płaszczyzny podstawy pod kątem 45 st?
Mathmi - tak myślałem, że coś zepsułem. Usunę zanim ktoś jeszcze mnie "zjedzie" :P
Chudy --> Jak skracałeś silnie przez siebie, to na górze powinno raczej zostać (n-1)n (bo skraca się (n-2)!, a n!=(n-2)!(n-1)n). Z tego wychodzi więc równanie n^2-n-132=0, co daje rozwiązanie -11 oraz 12. Jako że interesują nas raczej liczby dodatnie, to zostaje 12.
http://www.wolframalpha.com/input/?i=%28n+choose+2%29+%3D+66
$Respect$ -->
Zad. 1
http://www.wolframalpha.com/input/?i=%28x%2B3%29%28x-1%29%5E2%284-x%29%3E0 - odpowiedź do zadania jest w sekcji "integer solutions"
O, nie wiedziałen nawet, że istnieje taki temat :) Miło.
Wskaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku
Z góry dzięki ;)
1. Liczbę: 2/9! + 2/(7! * 3!) + 1/(5! * 5!) (nawiasy, żeby było wiadomo, że to razem w mianowniku), przedstaw w postaci 2^a/b!, gdzie a, b E N.
2. Uzasadnij, że dla dowolnych liczb a i b prawdziwa jest nierówność:
a^2 + b^2 + 4>= 2(a + b - ab)
3. Uzasadnij, że dla każdej liczby naturalnej n liczna n^3 + 5n jest podzielna przez 6.
Jakieś propozycje? Jak do tego podejść? Nie lubię zadań typu uzasadnij/wykaż ;| Wyglądają stosunkowo łatwo, ale ani tak, ani tak nic mi wyjść nie chce..
mnichu3001 -> To jedna z własności trójkątów, to się po prostu wie, nigdy nie próbowałem tego udowadniać.. Próbowałbym coś z podobieństwem trójkątów/twierdzeniem Talesa.
Edit:
Dobra, do tych, które pochylone znalazłem rozwiązanie.. Łatwe zadania jak już sie znajdzie sposób.. Może macie jakieś rady odnośnie zadań z uzasadnianiem właśnie? Jak do nich podchodzić? Na co zwracać uwagę?
Sage --> Jak przeniesiesz wszystko na lewą stronę, to możesz zauważyć, że da się to zwinąć do postaci (a+b-1)^2+3>=0. Jak wiadomo, każda liczba rzeczywista podniesiona do krawatu jest większa/równa od zera, kwadrat powiększony o 3 jest tym bardziej większy od zera. Tak więc dla każdej pary liczb rzeczywistych dana nierówność jest prawdziwa.
A jakieś porady? No nie wiem, zadania tego typu są rozmaite. Jeżeli jednak pojawiają się jakieś takie nierówności do udowodnienia to bardzo często sprowadza się to do szukania jakichś wzorów skróconego mnożenia, przekształcania do funkcji kwadratowych i liczenia delt, sprowadzanie do wielomianów czy funkcji wymiernych. Trzeba kombinować i już :)

Mam pytanie o wykres funkcji logarytmicznej
Polecenie jest takie, że mam odczytać znak liczby logarytmu, który jest na screenie.
Rysuję wykres, podstawiam pod x jakąś liczbę i przenoszę to na oś y. Co dalej? CO trzeba potem zrobić?
Mathmi -> Zazwyczaj większość sprowadza się do wzorów skróconego mnożenia czy tam delt. Jak w geometrii wszystko opiera się na trójkątach, tak algebra na tychże wzorach. Niestety jestem z tych, którzy muszą przeczytać zadanie i się z nim przespać.. Oczywiście mowa o tych nieco trudniejszych. Po chwili spędzonej na namyśle, nawet obliczeń nie muszę robić.. Tyle, że ten sposób się nie sprawdzi na egzaminie :| No nic, kupiłem przedwczoraj dwie książki z tymi trudniejszymi zadaniami i "ryję" jak nigdy w życiu.. Od wczoraj z 7h już będzie jak robię bez przerwy.. Może przez zmęczenie (6h spania, 9h poza domem, godzinny marsz w jedną stronę przy minus 9 stopniach..) nie zauważam już prostych rozwiązań i za bardzo kombinuję.. No nic, dzięki za odpowiedź. W razie wątpliwości będę pisał :)
TPU -> Mógłbyś napisać dokładną treść? Bo coś nie mogę złapać o co pytają..
Określ znak liczby: log (ten logarytm jest napisany na screenie)
I niby też jest sposób bez wykresu, że się sprawdza x i p.
Łatwo zauważyć, że log7(1)=0 (bo 7^0=1). Jednocześnie, logarytm o podstawie większej od 1 jest funkcją ściśle rosnącą. Skoro zatem 1/60<1, to log7(1/60)<log7(1)=0. Zatem badany logarytm jest mniejszy od 0.
Na wykresie możesz to w ten sam sposób pokazać. Skoro y=0 dla x=1, a 1/60 leży na lewo od 1, no to ten logarytm jest mniejszy od zera.
Możecie mi wytłumaczyć jak najłatwiej udowodnić, że jakaś funkcja jest odwracalna? Bo rozumiem, że trzeba wykazać, że jest ona bijekcją, czyli suriekcją i iniekcją. Z różnowartościowością to jeszcze spoko, ale to, że jest funkcją "na", to już jakaś głupota. Trzeba to udowadniać w ogóle? Czy narysowanie wykresu funkcji jest wystarczającym dowodem, że można ją odwrócić?
Tylko nie chodzi mi o jakieś gimnazjalne wytłumaczenie, tylko takie raczej profesjonalne - na poziomie matematyki na studiach dziennych - i to nie marketing ;)
jagged => Dla stosunkowo prostych funkcji w zupełności wystarczy stwierdzenie "na oko widać, że..." ;) (ewentualnie połączona z wykresem) Dla nieco bardziej skomplikowanych wypadałoby przeprowadzić jakieś wnioskowanie, np. udowodnić (uzasadnić) ciągłość na przedziale/na całej dziedzinie i podać ekstrema. Coś w ten deseń :)
jagged ==> Nie, ale przykładowo jeśli przeciwdziedzina jest przedziałem (domkniętym), to (oprócz wykazania różnowartościowości) wystarczy pokazać, że funkcja jest ciągła i osiąga ekstrema będące krańcami przedziału będącego przeciwdziedziną. Podałem jedynie przykład w jaki sposób można podejść do wykazywania suriektywności niektórych funkcji.
Łysy ==> Przemyśl to ;) (ekstremum nie koniecznie musi oznaczać, że funkcja tam "zawraca" - równie dobrze może się tam "urywać")
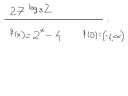
Mam takie dwa małe problemy. Problem nr 1 ( ten wyżej ) jest taki, że w mojej książce nie ma wytłumaczonego działania na takim logarytmie i nie wiem jak się zabrać za rozwiązanie ( wiem, że to proste, miałem to już rok temu ale po prostu nie pamiętam zasady ). Wynik to 8 jak coś ( z odpowiedzi książki ).
A w tym drugim zadaniu problem jest taki, że mam tam wyznaczyć wartość tej funkcji i miejsce zerowe. Z miejscem zerowym sobie poradziłem ale nie rozumiem dlaczego wyszła taka dziedzina jaką zapisałem ( z odpowiedzi z książki ). Przecież mogę podstawić każdą liczbę i wówczas dziedzina będzie (IMO), od minus nieskończoności do plus nieskończoności. Dzięki za pomoc.
EDIT - kretyn ze mnie, to 2 to przecież funkcja kwadratowa. W takim razie liczę na odpowiedź tylko do 1.
sokrates92 --> To drugie to nie jest funkcja kwadratowa, tylko wykładnicza. A to, co jest z boku napisane, to nie jest dziedzina, tylko zbiór wartości (masz tam f(D) czyli wartości funkcji f dla całego zbioru D - dziedziny). Funkcja wykładnicza przyjmuje jedynie wartości dodanie, więc przesunięta o 4 do dołu przyjmuje wartości większe od -4.
Co do pierwszego, to jak rozumiem, ten logarytm jest w potędze? No to logarytm jest funkcją odwrotną do funkcji wykładniczej. Tak więc a do potęgi logarytm o podstawie a się wzajemnie "znoszą". Musisz to więc przekształcić do takiej postaci, by na dole była potęga 3 (bo w logarytmie masz za podstawę 3). No więc:
27=3^3.
(3^3)^(log3(2)) --> jak potęgujemy potęge to mnożymy wykładniki
3^3log3(2) ---> 3log3(2)=log3(2^3)
3^log3(8)
8
koniec ;)
Mathmi Thenthur--> Mogę Cię prosić o wpisanie się do listy zawartej we wstępniaku? Zależy mi na tym choćby z tego względu, żeby owy wstępniak był cały czas w miarę aktualny, a przy tym również przejrzysty. Tak więc lista:
GOL-owi matematycy:
- lajtowy ziomek:) | Ogólnie: zakres wiedzy obejmujący materiał do klasy 3 Liceum. Chętnie pomogę z funkcji kwadratowej oraz wszelkich równań, nierówności. Słabość - Geometria. :P
- Filevandrel | Cały materiał LO i materiał z 2 lat studiowania elektroniki, łapać na maila [email protected] zawsze chętnie odpiszę!:)
- tomazzi | podstawówka, gimnazjum, liceum, co nie co ze studiów. Lubię zadania na rozkminkę :P
- DEXiu | cały zakres do szkoły średniej włącznie; matematyka "wyższa" na poziomie studenta uczelni technicznej (nie matematyki na uniwerku:) - mat. dyskretna, geometria, analiza, algebra, statystyka, probabilistyka; bardzo chętnie zadania i zagadki logiczne
- Maco | Zakres do LO i troszkę matematyki wyższej | Pięta achillesowa - trygonometria
- $ebs Master | Zakres - liceum, studia bez prawdopodobienstwa
- Łysy. | Cała rozkminka aż do liceum, szczególnie lubię geometrię. Potem analiza, algebra, podstawy dyskretnej, podstawy probabilistyki.
GOL-owi matematycy:
- lajtowy ziomek:) | Ogólnie: zakres wiedzy obejmujący materiał do klasy 3 Liceum. Chętnie pomogę z funkcji kwadratowej oraz wszelkich równań, nierówności. Słabość - Geometria. :P
- Filevandrel | Cały materiał LO i materiał z 2 lat studiowania elektroniki, łapać na maila [email protected] zawsze chętnie odpiszę!:)
- tomazzi | podstawówka, gimnazjum, liceum, co nie co ze studiów. Lubię zadania na rozkminkę :P
- DEXiu | cały zakres do szkoły średniej włącznie; matematyka "wyższa" na poziomie studenta uczelni technicznej (nie matematyki na uniwerku:) - mat. dyskretna, geometria, analiza, algebra, statystyka, probabilistyka; bardzo chętnie zadania i zagadki logiczne
- Maco | Zakres do LO i troszkę matematyki wyższej | Pięta achillesowa - trygonometria
- $ebs Master | Zakres - liceum, studia bez prawdopodobienstwa
- Łysy. | Cała rozkminka aż do liceum, szczególnie lubię geometrię. Potem analiza, algebra, podstawy dyskretnej, podstawy probabilistyki.
- Mathmi Thenthur | matematyka na poziomie szkoły średniej plus studia ekonomiczne: analiza, algebra, statystyka, rachunek prawdopodobieństwa; wybitnie nie lubię geometrii
Jak wszyscy, to wszyscy ;)
GOL-owi matematycy:
- lajtowy ziomek:) | Ogólnie: zakres wiedzy obejmujący materiał do klasy 3 Liceum. Chętnie pomogę z funkcji kwadratowej oraz wszelkich równań, nierówności. Słabość - Geometria. :P
- Filevandrel | Cały materiał LO i materiał z 2 lat studiowania elektroniki, łapać na maila [email protected] zawsze chętnie odpiszę!:)
- tomazzi | podstawówka, gimnazjum, liceum, co nie co ze studiów. Lubię zadania na rozkminkę :P
- DEXiu | cały zakres do szkoły średniej włącznie; matematyka "wyższa" na poziomie studenta uczelni technicznej (nie matematyki na uniwerku:) - mat. dyskretna, geometria, analiza, algebra, statystyka, probabilistyka; bardzo chętnie zadania i zagadki logiczne
- Maco | Zakres do LO i troszkę matematyki wyższej | Pięta achillesowa - trygonometria
- $ebs Master | Zakres - liceum, studia bez prawdopodobienstwa
- Łysy. | Cała rozkminka aż do liceum, szczególnie lubię geometrię. Potem analiza, algebra, podstawy dyskretnej, podstawy probabilistyki.
- Mathmi Thenthur | matematyka na poziomie szkoły średniej plus studia ekonomiczne: analiza, algebra, statystyka, rachunek prawdopodobieństwa; wybitnie nie lubię geometrii
- jagged | Zakres szkoły średniej + semestr informatyki na EAIiE (AGH) + wciąż studia informatyczne na Politechnice
Obliczyć pole powierchni pomiędzy funkcjami ln(x) i ln^2(x). Wychodzi całka oznaczona od 1 do e (ln(x)-ln^2(x))*sqrt(1+((1-2ln(x))/x)^2 dx. Nawet wolfram nie daje rady, a ja to muszę zrobić na za godzinę.
Fuck, źle przeczytałem i źle liczyłem, a tu napisałem dobrze. Cały czas myślałem, że chodzi o pole bryły obrotowej... Teraz to już jest banalne.
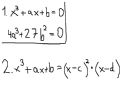
Wykazac, ze gdy rownanie 1. ma podwojny pierwiastek, to zachodzi rownosc 4*a^3 + 27*b^2.
Zaproponowano nam rozwiazanie 2., otrzymuje uklad rownan:
a=c^2+2*c*d
b=-c^2*d
Nie za bardzo wychodzi. Przynajmniej mi.
O matko:D nawet tutaj matma mnie prześladuje. Jakby było za mało, że przeze mnie cała klasa ma kartkówki co tydzień nie licząc ciągnących się matur na lekcjach co środę na 3 godzinach (normalnie punktuje i za każdą stawia ocenę, nie przepuści do matury jak się ich wszystkich nie pozalicza). Szkoda mi słów...
Lara--> Znam ten ból... również jestem w klasie maturalnej, tak więc maratony z nimi w roli głównej to u nas normalka (nawet jutro piszę z nomen omen z matmy maturkę ;P). No ale żeby co tydzień!? No nie... może i cisną mnie i resztę uczniów w mojej sql, no ale żeby aż tak, to nie. ;P
@pajkul
Jeszcze jest trzecie równanie:
-2c-d=0
lara i ziomek - a jak ja was oboje rozumiem, tyle że ja nic nie kumam i na 100% w maju nie zdam matury, tylko się wieszać.Z polaka miałem 80% z angola 83% a z matmy 12%..nosz kurde idzie się załamać, co mi po polaku i angolu jak maty nie zdam a z nią cała matura w błoto.
ale może ktoś pomoże mi (wytłumaczy) takie oto zadanie:
no więc jest takie zadanie:
Który z podanych ciągów jest ciągiem arytmetycznym?
a): bn = 5-2n
b): dn = 5-2n
c): fn=3n2(do kwadratu) -1
d): gn=(1-2n)2(do kwadratu) +4(1-n2(do kwadratu))
mam pytanie takie, że aż wstyd zadać, chodzi mi właściwie o upewnienie się.
Mam jednomian -7x + 2mx - 5m + 4 w liczniku a -2 w mianowniku, to przyrównując do zera zajmujemy się tylko licznikiem podpietym do zera, inaczej mówiąc tylko licznik przyrównujemy?
Jeśli tak to robiąc dalej z treści zadania wychodzi mi nierówność do parametru"
licznik -> 5m-4
mianownik -> -7+m
a cały ułamek jest mniejszy lub równy zeru - teraz przyrównuje kolejno licznik i mianownik do =< 0 ?
@37 tak, bo niezależnie przez co podzielisz 0, to zawsze będzie 0 np. 0/9=0 0/23234=0 :)
odświeżam drugą część pytania i dorzucam kolejne:
Rozkładam wielomian: x^4 - 6x^3 + 9x^2 + 4x - 12
1. Z grupowania wyszło mi coś takiego:
x^2*(x-3)^2 + 4(x-3)
I nie wiem co zrobić, bo gdyby pierwszy nawias był bez kwadratu no to luzik, ale w takiej sytuacji znowu jakaś czarna plama :(
^
Bardzo dobrze Ci wyszło. Teraz wyciągasz (x-3) tak jakby tam nie było kwadratu i wychodzi Ci:
(x-3)(x^3-3x^2+4). Teraz zauważasz, że dla jakiegoś tam x drugi czynnik się zeruje i wychodzi ładny wynik :)
spoiler start
(x-3)(x+1)(x-2)^2
spoiler stop
[37]
licznik -> 5m-4
mianownik -> -7+m
a cały ułamek jest mniejszy lub równy zeru - teraz przyrównuje kolejno licznik i mianownik do =< 0 ?
Nie, otrzymujesz nierówność, którą przekształcasz tak, aby otrzymać x. Czyli masz (w mianowniku mi wyszło 2m-7):
x <= (5m-4)/(2m-7)
x <= 5/2 + 27/(4m-14), meR\‹7/2›
Rozpisujesz wariacje, kombinację i liczysz. Co tam trudnego jest?
(n+2)! to inaczej (n+2)(n+1)n!
O boze. Chodzi mi o to, ze mam zbior n+2 - elementowy. Biore 2 elementy z tego zbioru bez powtorzen i chce wiedziec na ile sposobow moge wyciagnac te 2 elementy, nie wazna kolejnosc.
Czy moge to zrobic albo tak jak napisalem po lewej stronie rownosci albo jak po prawej stronie? Czyli wariacjami tak jak napisalem albo kombinacja. Problem w tym, ze wariacjami wychodzi 2x wiecej mozliwosci od tych z kombinacjami, co mnie dziwi.
nie wazna kolejnosc
W wariacjach kolejność jest ważna dlatego wychodzi Ci dwa razy więcej niż kombinacji. Dla kombinacji AB i BA to to samo, dla wariacji nie.
Permutacje - wszystkie elementy zbioru, ważna kolejność.
Wariacje - część zbioru, ważna kolejność.
Kombinacje - część zbiory, kolejność nie ważna.
No i bez sensu jest używanie takich rzeczy jeżeli chcemy wylosować jeden element :) (chodzi o wariacje, logiczne przecież, że ze zbioru n-elementowego mogę wyciągnąć n elementów :) )
Dziedziną funkcji f(x)=1/x^2-m^2+1 jest zbiór liczb rzeczywistych. Wyznacz przedział, do którego należy parametr m.
@Down
Nawiasu tam nie ma. Dzięki za pomoc ;]
[46]
Domyślam się, że tam powinien być nawias i wzór wygląda tak:
f(x)=1/(x^2-m^2+1)
Wyliczasz dla x pierwiastki równania: x^2-m^2+1=0 i analizujesz dla jakich m jest to spełnione. W odpowiedzi piszesz dopełnienie do liczb rzeczywistych tego co Ci wyszło.
spoiler start
x=sqrt(m^2-1) lub x=-sqrt(m^2-1), więc:
m^2-1>=0
m>=1 lub m<=-1
Odpowiedź: me(-1,1)
spoiler stop
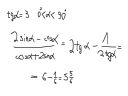
Odpowiedz prawidlowa to 5/7. Trzeba policzyc wartosc wyrazenia. A wychodzi 5 i 5/6.
napster92 ==> "Tam nie ma nawiasu" ale zapewne "tam" (w oryginalnej treści zadania) jest kreska ułamkowa, więc nawias jest niepotrzebny. Zapisując natomiast zadanie na forum, gdzie NIE MASZ kreski ułamkowej, tylko znak dzielenia, MUSISZ UŻYĆ NAWIASU! :/ jagged na szczęście domyślił się o co chodzi i dobrodusznie pomógł, ale gdyby był złośliwy, to by cię odesłał na bambus. Bo dziedziną funkcji f(x)=1/x^2-m^2+1 nie jest zbiór liczb rzeczywistych i parametr m nie ma tu nic do rzeczy.
pajkul ==> Zechcesz wyjaśnić jakim cudem przeskoczyłeś z tego, co jest po lewej stronie znaku równości do prawej? ;)
pajkul - 1/(2+3) to nie to samo co 1/2 + 1/3.
pajkul, litości :) Mam nadzieję, że to tylko tymczasowe zaćmienie, niewyspanie albo problemy natury prywatnej, a nie rażące braki z podstawówki. Od kiedy to można rozbijać MIANOWNIK ułamka? ;) Podziel sobie licznik i mianownik przez cos(alfa) i wyjdzie prawie natychmiast co miało wyjść ;)
DEXiu -> udzielasz pomocy również prywatnie? Pisałem na Twój nr gg, ale nie odpisałeś ;)
Ogólnie rzecz biorąc, mam zator z sesją spowodowany zadaniami z matmy, których, nie oszukujmy się, nie ogarniam. Do tej pory z zagadnieniami z matmy tj. logika, probabilistyka, radziłem sobie, ale obecny semestr mnie (w sumie wszystkich) całkowicie zmasakrował.
Oto te zadania: http://img153.imageshack.us/img153/2071/questforlife.jpg
Jeśli ktoś będzie mógł mi pomóc, proszę o kontakt na maila maviozo at poczta onet pl albo na jabberze maviozo at aqq eu
mav ==> Hm. Chyba nie dostałem Twojej wiadomości na gg w takim razie. Jednak irytuje zawodność tego środka komunikacji ;P Prywatnie w jakim sensie? :) Jeśli osobiście, to raczej nie. Natomiast w miarę wolnego czasu (na który nieszczególnie narzekam, ale chwilowo jeszcze mam, bo się semestr dopiero rozkręca) staram się pomagać czy to na forum czy via gg/mail/whatever :)
Co do zadanek, które wrzuciłeś - wyglądają na proste ;) Acz muszę sobie co nieco odświeżyć z metod numerycznych. Rzucę na nie okiem, ale to już nie dziś ;)
Prywatnie, w sensie poza forum ;) nie chcę zaśmiecać wątku
Klepnij do mnie maila, pisałem z nru gg 28631xxx, więc możliwe, że np. masz wersję, w której wysokie numery nie dochodzą.
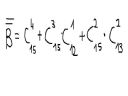
W pudelku znajduje sie 15 par rekawiczek, wsrod ktorych dowolne dwie pary roznia sie od siebie. Z tego pudelka wybieramy losowo cztery rekawiczki.
Oblicz prawdopodobienstwo zdarzenia:
B - wsrod wylosowanych rekawiczek nie ma ani jednej pary.
Szukalem w necie, ale nie moge znalezc wyjasnienia co do sposobu okreslania mocy zbioru B.
Jak dla mnie to: nie moze byc zadnej pary, a wylosowac mozemy albo 4 rekawiczki lewe/prawe, albo 3 rekawiczki lewe/prawe i 1 prawa/lewa, albo 2 prawe/lewe i 2 lewe/prawe. Jakby to zapisac uwzgledniajac to, ze odrzucamy rekawiczki do pary:
Wg mnie jakoś tak - pierwszą rękawiczkę wybieramy na 30 sposobów - bo jest ona dowolna. Drugą na 28 - bo jedna już jest wybrana i nie może być od tamtej pary. Trzecią na 26 - j.w. Czwartą na 24 - również j.w. Całość to: 30*28*26*24, czyli duużo. Teraz dzielimy to przez dowolne wybranie 5 rękawiczek z 30, czyli (30 nad 5) i mamy wynik.
spoiler start
640/87 = ok. 3,678
spoiler stop
Prosilbym jeszcze raz o wytlumaczenie mi dlaczego to, co zapisalem w [57] jest zle i jak zrobic dobrze.
spoiler start
Hehe.
spoiler stop
^
Czego nie rozumiesz w tym co zapisałem w poście 58.?
W Twoim rozumowaniu losujesz ciągle tylko z połowy wszystkich rękawiczek, od razu zakładając, że żadnej z pary nie wybierzesz. Nie wiem czy to moje rozwiązanie jest prawidłowe, ale większość zadań z prawdopodobieństwa właśnie tak rozwiązywałem - na chłopski rozum - a nie wzorami.
Pierwszą rękawiczkę wybieramy dowolną ze wszystkich. Drugą też dowolną, ale już tylko ze zbioru 28 (bo jedna już wylosowana i nie możemy dobrać pary tej rękawiczki). Trzecią też dowolną ze zbioru 26 (bo wszystkich rękawiczek zostało 28, ale dwie odrzucamy też, bo są do pary tych już wylosowanych). I czwartą wybieramy z 24 możliwości, bo zostało 27 wszystkich, ale 3 pasują do pary do już wylosowanych. Jest to za każdym razem wybór 1 elementu ze zbioru, więc prawdopodobieństwem jest po prostu ten zbiór. Tworzymy iloczyn i tyle, bo innych możliwości nie ma.
@pajkul
Ja bym to zrobił tak:
Jeśli każdą rękawiczkę można wylosować z tym samym prawdopodobieństwem to:
Wybór pierwszej rękawiczki nie ma wpływu na wynik (bo mając 1 rękawiczkę nie możemy stwierdzić, czy wylosowaliśmy rękawiczkę do pary).
Przy drugiej rękawiczce możemy już to stwierdzić. Losujemy ją spośród 29 pozostałych rękawiczek. Aby wylosowana rękawiczka była nie do pary to musi być inna od tej pierwszej, a więc dowolną z 28 pozostałych. Czyli mamy 28/29
Przy trzeciej rękawiczce jest tak samo, poza tym, że pozostało 28 rękawiczek oraz 26 takich, które będą nie do pary z tymi już wylosowanymi. Czyli prawdopodobieństwo wylosowania 3 różnych rękawiczek wynosi:
(28/29)*(26/28)
Przy czwartej mamy 27 pozostałych i 24 nie do pary (z tymi już wylosowanymi), zatem sumarycznie mamy:
Prawdopodobieństwo wylosowania 4 różnych rękawiczek:
(28/29)*(26/28)*(24/27)=(26/28)*(8/9)~= 0,825
(znak ~= znaczy w przybliżeniu równa się)
"W Twoim rozumowaniu losujesz ciągle tylko z połowy wszystkich rękawiczek, od razu zakładając, że żadnej z pary nie wybierzesz."
Jest 15 tylko dlatego, ze zdarzenie ze wylosuje 4 rekawiczki z jednej grupy (albo z grupy lewych albo z prawych) traktuje jako jedno, a nie dwa. Nie wazne z ktorej grupy, liczy sie efekt, tak przyjalem. Nie jestem wlasnie pewien czy to poprawnie. A moc omegi to policzylbym do tego jako kombinacja 4 z 30. Tez pytam, czy moge tak postapic.
jagged ==> PRAWIE dobrze ;) A "prawie" dlatego, że w ten sposób zakładasz, że kolejność losowania jest ważna (w Twoim modelu wylosowanie rękawiczek w kolejności A, B, C, D i D, A, C, B to dwie różne możliwości), natomiast moc zbioru wszystkich zdarzeń liczysz jako kombinacje (czyli kolejność nieważna). Żeby było ok podziel sobie ten wyliczony iloczyn przez 4! ;) Aha. I moc zbioru wszystkich zdarzeń chyba nie 30 po 5, tylko po 4 :) Zresztą już sam fakt, że prawdopodobieństwo wyszło Ci 3 z czymś (>1) powinno dawać do myślenia, że coś jest nie tak ;)
pajkul ==> Nie możesz przyjąć, że sobie będziesz rozpatrywał tylko przypadek wylosowania 4 lewych, później 3 lewych i 1 prawej i na koniec 2 lewych i 2 prawych - musisz uwzględnić wszystkie przypadki ALBO podzielić ostatni składnik (2 lewe i 2 prawe) przez 2 (oraz moc zbioru wszystkich zdarzeń też przez 2 wtedy). Wyjdzie to samo co jaggedowi (po poprawce ;)
Podzielic [kombinacja 2 z 15 * kombinacja 2 z 13] przez 2, bo jak na razie biore pod uwage takze kolejnosc? Podobnie w mocy omegi? Nie wiem czy dobrze rozumiem.
Zresztą już sam fakt, że prawdopodobieństwo wyszło Ci 3 z czymś (>1) powinno dawać do myślenia, że coś jest nie tak ;)
Dawno już nie miałem prawdopodobieństwa, więc nawet nie wiem co to wyliczam :D
Czyli powinno być już poprawnie - o, tak:
21840/27405 = ok. 0,8
pajkul ==> Nie do końca. Podzielić musisz przez 2, bo jakbyś NORMALNIE liczył (a nie wydziwiał), to policzyłbyś tak:
1 raz przypadek, gdy 4 lewe
1 raz przypadek, gdy 1 lewa i 3 prawe
1 raz przypadek, gdy 2 lewe i 2 prawe
1 raz przypadek, gdy 1 prawa i 3 lewe
1 raz przypadek, gdy 4 prawe
Zauważ, że dwa pierwsze i dwa ostatnie przypadki są tożsame (tylko że symetrycznie zamieniasz lewa z prawą), natomiast środkowy przypadek (2 takie i 2 takie) nie ma swojego symetrycznego odpowiednika. Stąd przeskalowanie przez 2 tego przypadku oraz mianownika ułamka. Ogólnie to dość trudno wytłumaczyć. I dlatego właśnie uważam, że takie cudowanie "a policzę sobie tylko taki przypadek" szkodzi a nie pomaga.
DEXiu->i co z tymi zadaniami? Mam jeszcze tydzień tylko na zrobienie tego - ba, jeszcze trzeba do jednego z nich napisać "program", który to oblicza. Napisz do mnie maila (maviozo at poczta onet pl) , dla mnie to naprawdę szalenie ważne.
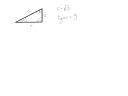
Tu znowu ja. Mam problem z jednym zadaniem. ---------------------------------->
Trzeba wyliczyć A i B.
Z podstawowych własności nie można tego wyliczyć, bo ani z tg, ani ctg się tego zrobić nie da. Próbowałem z jedynki trygonometrycznej wyliczyć jakoś b albo a, ale poległem na funkcji kwadratowej, która nie dała żadnego poprawnego rozwiązania. Tak więc nie mam pomysłu jak się do tego zabrać. Próbowałem z tg, ctg bety, ale jest to samo co w alfie. Dodam, że są to jedyne dane, które podałem.
Wiem, że dla was to pewnie bułka z masłem więc... z góry dzięki za pomoc :P
Łysy - musiałbym mieć to a lub b żeby tak liczyć (chyba).
EDIT.
mój błąd, już rozumiem. Dzięki łysy :)

Ostatnie 2 zadania i już was nie męczę. Myślałem nad nimi ale nie rozumiem o co w nich chodzi.
-------------------------------------------->
W pierwszym nie rozumiem słowa ''rozwiązania'', chodzi o miejsca zerowe czy co ? Jeśli tak to mi wychodzi jedno a odpowiedź prawidłowa to D.
W drugim zadaniu nie wiem o co chodzi, gdyż zawsze kąt miałem podany i nie wiem jak się do tego zabrać.
Możecie tylko podpowiedzieć co i jak, obliczę sam.
Tak, możesz na pierwsze zadanie patrzeć, jak na szukanie miejsc zerowych. Musisz sobie wszystko przerzucić na jedną stronę i przekształcić do postaci funkcji kwadratowej. Wyjdzie Ci wtedy, że rozwiązania faktycznie są dwa.
Co do drugiego. Napisz sobie, ile wynosi sin30 i sin60. Porównaj te wartości z 0,8. Narysuj sobie wykres sinusa i zobacz, gdzie powinien leżeć kąt, dla którego sin wynosi 0,8 (sprawdź, czy to będzie jeden z tych katów, czy będzie na lewo, na prawo).
Ale do czego Ci ten cosinus potrzebny? Musisz określić, mniej więcej, jaką miarę ma kąt, którego sinus wynosi 0,8.
Podpowiem Ci, że sin60=sqrt(3)/2, czyli mniej więcej 0,87, czyli więcej niż 0,8. Teraz weź sobie to narysuj czy coś i pomyśl, jaki możesz wniosek wysnuć z tego, że sin60 (ten kąt pojawia się w odpowiedziach) wynosi więcej niż 0,8.
[75] No bo jeżeli wiem, że cos alfa jest ok 0,565 to z tablic odczytuje że cos 56 alfa = 56stopni alfa ( akurat taka zbieżność wyszła ).
No tak, tyle że w ten sposób, to możesz sobie od razu wziąć z tablic dla jakiego kąta mniej więcej sinus wynosi 0,8 i w ogóle nic nie rozumieć o co chodzi.
Pomijam fakt, że źle wyliczyłeś ten cosinus, gdyż 100-64, to nie jest 32. A sin56, to 0,829.
[72]
Najłatwiej narysować sobie sinus od 0 do pi/2, czyli tam gdzie jest ostry, i zauważyć, że jest to funkcja rosnąca. Teraz liczymy sinus odpowiedzi A i sprawdzamy jak się on ma do 0,8. Jeśli jest równy - to koniec zadania, jeśli jest mniejszy - to znaczy, że poprawną odpowiedzią jest B, C lub D. Potem liczymy sinus odpowiedzi C i sprawdzamy znów jak się on ma do 0,8. Jeśli jest równy - to odpowiedzią jest C, jeśli mniejszy - to odpowiedzią jest D, jeśli większy - to odpowiedzią jest B.
spoiler start
sin(30) = 1/2, 1/2 < 4/5
sin(60) = pierw(3)/2, pierw(3)/2 > 4/5
odp. B.
spoiler stop
Ok nareszcie zrozumiałem. Dzięki chłopaki, ciężko mi było zrozumieć z tego jak to tłumaczyliście słownie ale spoiler z [78] otworzył mi oczy.
Dzięki.
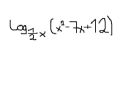
Panowie, jakie założenia na dziedzinę funkcji tutaj muszą być?
To, że x^2-7x+12 > 0, to na pewno.
A na podstawę logarytmu chyba też? Tylko jakie? Założenia, że funkcja jest rosnąca lub malejąca? Czyli 1/2x > 1 v 1/2x > 0 i 1/2x <1? Prosiłbym o oświecenie, bo ogólne założenia chyba znam, ale nie wiem, czy to w klamerce, czy jak? :)
Dobra, jest dobrze ;) Dzięki :)
Mam dwa zadania, ale na razie zapodam jedno, z którym mam największy kłopot:
Papierowe koło o r=15cm rozcięto na połowy i z każdej z nich zwinięty stożek, przeznaczając wycinek o 1/6 powierzchni półkola na zakładkę. Jaka jest V stożka?
Mianowicie chodzi mi o r jednego z tych kół po przecięciu. 7,5cm? :)
A co do drugiego zadania -
Z 27 takich samych kulek o r=2m zrobiono jedną kulę. Ile razy P tej większej jest większy od P jednej z tych mniejszych.
Ja liczę pole tej jednej małej, mnożę przez 27 i mam pole większej, ale to liczenie kompletnie bez sensu.
[83]
Promień jednego koła po przecięciu wynosi 7,5 cm (nie potrafiasz podzielić 15 przez 2?).
Jak robiono tę drugą kulę? Tak, że po prostu posklejano te mniejsze do siebie i zostały gdzieniegdzie takie puste miejsca? Jeśli tak, to pole większej kulki jest 27 razy większe niż mniejszej kulki. Ale zapewne jakoś inaczej ją tworzono.
edit. Jeśli przetopiono, to liczymy objętość małej kulki, mnożymy przez 27 i mamy objętość dużej kuli. Teraz z objętości możemy wyznaczyć promień, który będzie nam potrzebny do wyliczenia pola powierzchni, który następnie porównujemy z P małej kulki, które wynosi 16pi.
takie małe zadanko z którym ma problem
Obliczyć :
lim x->0- ctg (x) - 1/x
Robię to tak:
1/tgx - 1/x = x-tg/xtgx i z L'Hospitala lecę dalej ->
(1- 1/cos^2x) / (tgx/cos^2x) i po tym znowu L'H i wychodzą mi niestworzone rzeczy. Gdzieś jest błąd?
Mam dwa zadania, ale na razie zapodam jedno, z którym mam największy kłopot:
Papierowe koło o r=15cm rozcięto na połowy i z każdej z nich zwinięty stożek, przeznaczając wycinek o 1/6 powierzchni półkola na zakładkę. Jaka jest V stożka?
Mianowicie chodzi mi o r jednego z tych kół po przecięciu. 7,5cm? :)
???
Czy jak rozetniesz jabłko na pół, to dostaniesz dwie połówki jabłka, czy dwa mniejsze jabłka?
Masz więc półkole o r=15 cm. Intuicyjnie rzecz ujmując, masz 180st. w tym półkole, z czego 1/6 została przeznaczona na sklejenie stożka. Fragment powierzchni, który stanie się stożkiem na płaszczyźnie jest więc fragmentem koła o kącie 150st. Mając ten kąt jesteś w stanie policzyć długość łuku, czyli długość okręgu podstawy stożka, dalej z niego R podstawy tegoż stożka, dalej z pitagorasa mając te 15 cm z wcześniejszego półkola wyliczasz h stożka i wzór na pole to już powinieneś znać.
zad 2
wyliczasz objętość małej kulki, mnożysz razy 27 (ich ilość) i masz objętość dużej kuli. Z tego podstawiasz do wzoru na objętość kuli, żeby wyznaczyć R, a potem mając R, wyznaczyc pole powierzchni kuli.
za to pole powierzchni 27 kulek to nic innego jak pole powierzchni jednej razy 27
[86]
L'Hospitala źle obliczyłeś. Licznik jest dobrze, tylko w mianowniku coś poplątałeś.
Rozwiązanie:
spoiler start
ctg(x) - 1/x
(x - tg(x)) / (x * tg(x)) H
(1 - 1/cos^2(x)) / (tg(x) + x * 1/cos^2(x))
(cos^2(x) - 1) / (tg(x) * cos^2(x) + x) H
sin(2x) / (tg(x) * sin(2x) + 1)
lim x->0- z powyższego = 0
spoiler stop
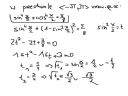
Czy dobrze rozwiazuje? Bo jakos tutaj:
http://matematyka.pisz.pl/forum/40932.html
nie maja rozwiazania 1/2. Bo sa tutaj dwie mozliwosci: albo sinus (-+)pierw z 3/2 albo cosinus. I w obydwu przypadkach wartosc drugiej funkcji to (-+)1/2
1.Które zdanie jest nieprawdziwe?
a-każde dwa romby są podobne
b-każde dwa trójkąty równoboczne są podobne
c-każde dwa okręgi są podobne
d-każde dwa kwadraty są podobne
2.Trójkąt A'B'C'(prim) o polu 24cm^2 jest podobny do trójkąta ABC 3cm,4cm,5cm. Długość przeciwprostokątnej trójkąta A'B'C'(prim) wynosi:
a-20cm
b-10cm
c-16cm
d-8cm
3.Powierzchnia skweru na planie w skali 1:1000 jest mniejsza od powierzchni rzeczywistej tego skweru:
a-1000razy
b-2000razy
c-40 000razy
d-milion razy
Bardzobym prosił o rozwiązanie, bo na jutro;)
Nie wiesz co to figury podobne? Czy po prostu nie chce Ci się robić zadań i masz nadzieję, że ktoś je za Ciebie zrobi?
a, a (nie chce mi się liczyć), a (mam nadzieję, że jednostka to cm?)
Kurde 10 było.Zrobiłem, tylko do tych nie jestem pewny.Dobrą pójdę se na zadane.pl
Ja mam proste zadanie.
Jaki jest obwód ziemi na szerokości 53 stopni?
I jak to policzyć?
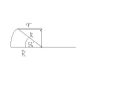
patrz na obrazek
R- promień Ziemi (przyjmujemy, że Ziemia to kula)
r - promien przekroju na szerokości 53 st.
90-53=37
sin 37st.= r/R
Łysy - dzięki.
Właśnie sobie uświadomiłem że straciłem sporo z danej dociekliwości matematycznej...
Mam znaleźć wartość p tak, by równania były do siebie równoległe. No więc stosowany jest wzór AB1 - A1B = 0. Dalej jest rozpisane tak:
p * (p+1) - 2 * 6 = 0
p^2 + p - 12 = 0
[trójkąt = delta] = 49, [pierwiastek z delty] = 7
p = -4 v p = 3
O co chodzi z tymi deltami? W książce nie jest to wyjaśnione, a ja mam dość spore braki i za cholerę nie mogę się domyślić rozwiązania.
hieronip
"mam spore braki"
Przespałeś połowę pierwszej klasy? Zerknij do podręcznika albo do Googli i poszukaj sobie o rozwiązywaniu równań kwadratowych.
pajkul [89]
Dobrze rozwiązujesz i oni też dobrze rozwiązują. Zauważ, że Ty masz sin albo cos połówki kąta równy odpowiednio +/- 1/2 albo +/- sqrt(3)/2, a oni mają sin albo cos całego kąta x. Jeżeli to rozwiążesz w zadanym przedziale wyjdzie Ci, że x = +/- 60 lub +/- 120 stopni. I u nich wyjdzie dokładnie to samo :)
proste zadanie - jednak nie moge sobie przypomnieć jak się coś takiego rozwiązuje :|
x^4 - 2x^3 - 3x^2 + 4x +4 <= 0
Totalna pustka :( - wszelkie porady mile widziane ;p
DEXiu -> To w koncu co ma byc w przedziale od minus pi do pi? x? Czy x/2?
Revanisko ---> Najpierw szukasz pierwiastka, który jest jednym z dzielników wyrazu wolnego czyli w Twoim przykładzie 4, 2, 1, (-1), (-2), (-4). Po prostu podstawiasz i sprawdzasz, która liczba wyzeruje Ci równanie. A później dzielisz wielomian przez (x - a) - gdzie a w moim przypadku jest pierwszym pierwiastkiem.
pajkul ==> Z reguły jak jest polecenie, aby rozwiązać równanie w jakimś przedziale, to (w domyśle) chodzi o to, że w tym przedziale jest niewiadoma. Co jest niewidomą: x czy x/2? W sumie to też konwencja, ale jednak x ;)
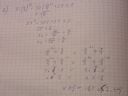
Takie pytanie jeszcze mam - w sumie z ciekawości
Dlaczego (tak jest według odp w książce) tam na samym końcu w jednym przypadku znak się odwraca ,a w drugim nie?
Z tego co wiem jeżeli podstawa jest w zakresie od 0 do 1 to się zmienia znak na przeciwny - a tu jednak wychodzi na to ,że raz się zmienia a raz nie :|
Revanisko ==> Bo się grzmotnąłeś w rozwiązaniu. W obu przypadkach się znak zmienia na przeciwny, tylko że w tym jednym, gdzie Ci się niby "nie zmienia" pomyliłeś jego zwrot już na wcześniejszym etapie ;)
Napisałeś tak:
t >= 3/2 lub t >= 9/4 (za t już podstawiłeś konkretną wartość, ale nie chce mi się tego przepisywać)
a powinno być:
t <= 3/2 lub t >= 9/4
Mam takie zadanko:
Uprość wyrażenie i wyznacz jego dziedzinę.
9 * x do kwadratu - 49
--------------------------
3 * x do kwadratu + 7x
---- to kreska ułamkowa
Wyszło mi, że dziedzina to wszystkie liczby rzeczywiste z wyjątkiem - 7 / 3
Co do uproszczenia to jedyne co mi przychodzi do głowy to wyjęcie czynnika przed nawias ale nie wiem czy to jest uproszczenie. Zrobiłem tak w mianowniku i wyszło 2x(1,5x + 3,5)
Będę wdzięczny za pomoc bo nie wiem czy dobrze jest to zadanie
Mianownik nie może być 0 więc liczysz miejsca zerowe.
Co do uproszczenia to licznik możesz rozbić na iloczyn zgodnie z wzorem (a^2 - b^2) = (a - b)*(a + b). Teraz wystarczy na dole coś wyciągnąć przed nawias i się skróci.
^ - to oznaczenie dla potęgi.
Hmm, no to w takim razie mam po części dobrze bo miejsce 0 jest tylko 1.
Co do tego wzoru, to nie iem za bardzo jak to z licznika (jezeli przeksztalce tak jak mowisz) skroci się z tym na dole.
Ale mam jesze jedno zadanie:
Rozwiąż równanie:
a)
x-1 / x+1 = -5/x+5
Wyszło mi tutaj, że rozwiązaniem rownania jest x= -9 oraz x=0
w nast przykładzie
b)
1/x+3 + x+3/x-3 = -6/x^2 -9
Trochę mi się pogmatwało i wyszło mi, że równanie nie ma rozwiązań, gdyż wyszło iż -4=0
Nast zadanie, tym razem prostsze:
Wyznacz c ze wzoru:
1/a -1/b = 1/c
Wyszło mi ze c = b-a/ab
i a,b,c nie mogą = 0
[114] :: a) dobrze, b) przepisz ładnie i rozwiąż jeszcze raz. Powinno wyjść x=-3, x=-4.
edit. [112]
Tak jak napisał Macco.
spoiler start
(9x^2 - 49)/(3x^2 + 7x) = [(3x-7)(3x+7)]/[x(3x+7)] = (3x-7)/x = 3 - 7/x, czyli xeR\‹0,-7/3›
spoiler stop
edit2. Wyznacz c ze wzoru:
1/a -1/b = 1/c
Wyszło mi ze c = b-a/ab
i a,b,c nie mogą = 0
Źle Ci wyszło. Wspólny mianownik lewej strony, odwrócenie obu ułamków, koniec.
jagged [115] - Zrobiłem inaczej i ładniej i z delty wyszło, że nie ma miejsc 0 (delta mniejsza niz 0).
Napiszę Ci jak to zrobiłem:
1/x+3 + x+3/x-3 = -6/x^2 - 9
x+3/(x+3)*(x-3) + (x+3)*(x+3)/(x-3)*(x+3) = -6/x^2 -9
x+3/x^2-9 + x^2 + 6x + 9/x^2 - 9 = -6/x^2 - 9
x^2 + 7x + 12/x^2 - 9 = -6/x^2 -9
x^2 + 7x +12 = -6
x^2 + 7x + 18 = 0
delta = b^2 -4ac
delta = 7^2 -4*18 = 49 - 72
delta = -23
Już w 2 linijce jest błąd. Wykonałeś przejście:
1/x+3 = x+3/(x+3)*(x-3)
a to nie jest to samo, gdyż licznik i mianownik musisz pomnożyć przez tę samą liczbę, jeśli tak chcesz sobie już utrudniać. Wspólny mianownik, przeniesienie wszystkiego na jedną stronę, pomnożenie przez mianownik i pamiętanie o tym, że jakiś tam x nie należy do dziedziny, rozwiązanie trywialnego równania kwadratowego.
I rób nawiasy w licznikach i mianownikach, bo nie wiadomo co jest w którym ułamku.
edit. Lecę, powinieneś poradzić, bo zadania są trywialne - jak to mawiają profesorowie - wystarczy tylko robić powoli i z głową ;)
edit2.
spoiler start
1/a - 1/b = 1/c
b/ab - a/ba = 1/c
(b-a)/ab = 1/c
c = ab/(b-a)
spoiler stop
Jagged [115] - odnośnie tego z wyznaczeniem wzoru na c.
Zrobiłem 2 raz i wyszło, że c=c*a
Móglbys moze podac Twój wynik i sposob w jaki do niego doszedłes?
Ahha, co do tego co się rąbnąlem w 2 linijce to już widzę co zrobilem źle :D No nic sproboję jescze raz uważniej.
Zadania trywialne, a na nich 26 osob na 30 miało jedynki :O
Mnie nie było w szkole wtedy ale trochę się dziwię dlaczego tak słabe wyniki z tego spr były. Dizęki za porady :)
Hmm, no to w takim razie mam po części dobrze bo miejsce 0 jest tylko 1.
A co się stanie jak za x podstawisz 0?
Co do tego wzoru, to nie iem za bardzo jak to z licznika (jezeli przeksztalce tak jak mowisz) skroci się z tym na dole.
Wyciągnij na dole x przed nawias to się skróci.
edit: dopiero teraz zauważyłem, że jagged napisał to samo w spoileprze.
To teraz ja proszę o pomoc :)
Ile jest wyrazów 10-literowych, ułożonych z liter ‹A,B,C,D› takich, że litera A występuje dokładnie 3 razy, B dokładnie 2 razy i C conajmniej 2 razy?
Zrobiłbym to z wariacjami, czyli tak:
A: 10!/7!
B: 7!/5!
C: 5!/3! lub 5!/2! lub 5!/1! (Gdy literek C jest 5, to znaczy, że wypełniają cały pozostały obszar, więc jest to jeden wybór.)
D: Dopełniam do całości, ale te same literki nie są rozróżnialne, więc zawsze jest to jeden wybór.
Całość wyglądałaby tak: (10!/7! * 7!/5! * 5!/3!) + (10!/7! * 7!/5! * 5!/2!) + (10!/7! * 7!/5! * 5!/1!) + (10!/7! * 7!/5!) = (10!/3!) + (10!/2!) + (10!/1!) + (10!/5!) = 6078240. Dobrze myślę? Jeśli nie, to niech mi ktoś wytłumaczy, gdzie robię błąd i pokaże różnicę pomiędzy wariacjami, kombinacja i permutacjami.
Ja to bym zrobił tak:
Najpierw losujesz 3 miejsca dla liter A, czyli kombinacja 3z10, potem losujesz 2 miejsca dla liter B czyli kombinacja 2z7, potem C kombinacja 2z5 i potem zostają Ci 3 miejsca w które możesz wrzucić 2 różne litery.
Później policzę. Masz gdzieś wynik jaki powinien wyjść?
201600? Tylko trzeba jeszcze odjąć powtarzające się ;/
...
edit. Ok, przecież te same literki są nierozróżnialne. Czyli jak to ma wyglądać? Możesz mi rozpisać ten ostatni punkt, czyli to wrzucenie 2 literek w 3 miejsca?
edit2. Wyszło mi 100800. Liczyłem to tak:
C(3z10)*C(2z7)*C(2z5)*8 = (10!*7!*5!*8)/(3!*7!*2!*5!*2!*3!), dobrze? :)
To powyżej powinno wyjść 201600, coś źle policzyłem. Ale i tak wydaje mi się, że poprawne jest to rozwiązanie:
(10 nad 3)*(7 nad 2)*(5 nad 2) + (10 nad 3)*(7 nad 2)*(5 nad 3) + (10 nad 3)*(7 nad 2)*(5 nad 4) + (10 nad 3)*(7 nad 2) = 65520
Z tego co ja kojarzę, to uczono mnie tak, że jak sobie robisz sumę prawdopodobieństw, to każdy kolejny składnik musi pokrywać całość*. U Ciebie np pierwszy składnik obsadza tylko 7 miejsc. Edycja: już rozumiem Twój sposób. Zaraz policzę swoim i powiem czy wyszło tak samo.
Po zastanowieniu się, zrobiłbym to tak:
Najpierw losujesz 3 miejsca dla liter A, czyli kombinacja 3z10, potem losujesz 2 miejsca dla liter B czyli kombinacja 2z7. Zostaje 5 miejsc, z czego przynajmniej 2 to C. No i sobie teraz te 5 miejsc musisz rozpisać. Wyszło tyle samo co u Ciebie. W sumie taki sam sposób liczenia tylko ja wyciągam (10 nad 3)*(7 nad 2) przed nawias :)
* wszystkie miejsca, wszystkie liczby, wszystkich pasażerów itp.
Witam.
Obrazem okręgu o1 w jednokładności o środku S i skali k jest okrąg o2. Wyznacz:
a) skalę jednokładności
b) współrzędne środka jednokładności, jeżeli:
o1: (x+1)^2+(y-2)^2=4
o2: x^2+y^2-6x-27 =0
Wyznaczyłem już:
o1: S(-1,2), r=2
o2: S(3,0), r=6
Co dalej? Próbowałem użyć wzorów, ale niezbyt mi to wychodzi. Może ktoś mi napisać w krokach, co należy zrobić? Będę wdzięczny.
Jeśli niezbyt wychodzi ci użycie wzorów, zacznij od porządnego rysunku.
Poradziłem już sobie ze skalą (k=3 v k=-3).
Mam pytanko, co do podpunktu b. Rozrysowałem sobie to. Środek leży na odcinku z So1 do So2, tak? Czyli co? Zrobić to wektorowo o1S = k* o2S ?
Wydaje mi się, że na samym odcinku leżeć nie może w tym przypadku, ale na prostej oznaczonej przez te dwa punkty już tak. Konkretnie to nie chce mi się liczyć nic, z rysunku widać, że to punkt (-3, 3)
Wyszło! Dzięki wielkie!
Granice nie są moją mocna stroną ....
Oblicz: robie z Hospitala i cały czas wychodzi mi 0/0 ...
lim x->o+ (1/sin^2x - 1/x)
Ok, tomazzi, dzięki wielkie :)
[134] :: lim x->0+ (1/sin^2x - 1/x) = lim x->0+ ((x - sin^2x)/(x*sin^2x)) =H= lim x->0+ ((1 - sin2x)/(sin^2x+x*sin2x)) = (1-0)/(0+0*0) = niesk.
[136] :: Musisz wyrazić wysokość h i promień r walca, za pomocą promienia R półkuli. Gdy to zrobisz, wstawiasz do wzoru na objętość walca i masz funkcję jednej zmiennej np. V=f(h) i liczysz dla tej funkcji ekstremum - czyli najłatwiej pierwszą pochodną przyrównać do 0. W tym punkcie objętość jest największa (jeśli wyjdzie Ci minimum, a nie maksimum, to coś źle przekształciłeś) i obliczyłeś właśnie wysokość h, dla jakiej ta objętość jest największa. Podstawiasz wysokość, aby obliczyć promień walca i masz wynik.
spoiler start
R^2 = h^2 + r^2
r^2 = 16 - h^2
V = pi*r^2*h = pi*(16-h^2)*h = -pi*(h^3-16h)
V' = -pi*(3h^2-16)
V' = 0 <=> 3h^2=16
h = 4*pierw(3)/3
r = 4*pierw(6)/3
spoiler stop
Dzięki już wiem gdzie leżał błąd. Pochodna z sin^2x to nie 2sinx ale sin2x.
Tutaj nie wie kompletnie jak się zabrać za to (gościu na wykładach robił podobne zadanie z działką przy murze, ale wyszedł mu wynik -20 m i dał sobie siana ...) więc nijak nie wiem jak się do tego zabrać...
1. W półkole o promieniu R=4 wpisano walec o największej objętości. Podaj wymiary tego walca
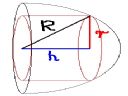
jedno pytanko, nie powinno być h^2/2 zamiast h^2?
O to chodzi?
edit. DEXiu :: Też się nad tym zastanawiałem i doszedłem do wniosku, że Max_101 popełnił literówkę ;) Dlatego napisałem w swoim poście: "Musisz wyrazić wysokość h i promień r walca, za pomocą promienia R półkuli.".
Max_101 ==> Przez dobrą minutę zastanawiałem się, co może oznaczać "w półkole wpisano walec" (jak w figurę płaską można wpisać bryłę) :] Czy przypadkiem nie powinno być "w półkulę..."?
Pewnie tak jest, zadania wysyłała mi znajoma. Na początku też myślałem jak to narysować, ale w końcu stwierdziłem, że półkula jest logiczniejsza ;)
Jeszcze jedno pytanko, przy liczeniu asymptoty ukośnej, a wyszło mi 0, a b = infinite. to znaczy, że taka asymptota nie istnieje, prawda?
I dzięki wielkie za pomoc, bardzo się przydała :)
Jeszcze jedno pytanko, przy liczeniu asymptoty ukośnej, a wyszło mi 0, a b = infinite. to znaczy, że taka asymptota nie istnieje, prawda?
Jeśli a=0 i b=liczba, to znaczy, że jest to szczególny przypadek asymptoty ukośnej, a mianowicie - asymptota pozioma. Ale skoro b wyszło nieskończoność, to znaczy, że asymptota ukośna i pozioma w tym punkcie nie istnieją.
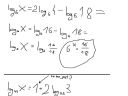
To znowu ja. Rozwiązuje sobie logarytmy i nagle mam taki przykład : -------------->
No i dochodze do momentu widocznego na screenie i nie wiem jak to się dalej liczy. Ma ktoś jakiś pomysł ?
A w tym drugim to właściwie chodzi o to samo ale zapisałem go bo nie wiem co to jest to '1' i jak to traktować ?
nie prosze o rozwiązania tylko o samo działanie. matura za miesiąc i trza zap....
edit. Zmieniłem nawiasy, żeby były analogicznie do polecanej na górze notacji matematycznej.
1 = log[x](x), gdzie pierwszy x w nawiasie kwadratowym to podstawa logarytmu, a ten w nawiasie okrągłym to liczba logarytmowana. Więc w Twoim przypadku 1 = log[0,5](0,5).
6^x = 16/18 = 8/9
x = log[6](8/9)
edit. BTW źle rozwiązałeś to zadanie. Gdy masz równość dwóch logarytmów o tej samej podstawie, to liczby logarytmowane się po prostu równają, więc x = 8/9 i koniec.
Cześć, możecie mi powiedzieć jak z równania Nernsta wyliczyć Ox i Red?
Równianie Nernsta:
http://upload.wikimedia.org/math/d/1/5/d158ce6e9290b56d09b288903382018a.png
Dwa prostokąty podobne maja po jednym boku równym 14 cm. Obwód mniejszego z tych prostokątów wynosi 44 cm. Oblicz odwód i pole drugiego prostokąta.
Tyle zrobiłem:
Obw = 44 cm, czyli 2a + 2b = 44 cm. W efekcie daje to to, że b = 8cm. Czyli ten mniejszy ma boki 14 cm i 8 cm.
Co dalej zrobić, bo zupełnie się zaciąłem. Jakieś pomysły?
Pytający - poszło na gg :)

Zadanie latwe, ale klucz mnie zdemotywowal :))
Skad te zalozenia ze a1 lub r nie moze byc rowne zero ?
Dalej nie rozumiem... W rownaniu w mianowniku mamy a1+r i a1+4r a wiec
a1 != -r
i
a1 != -4r
z pierwszego wynika ze jezeli r = 0 to a nie moze sie rownac zero, to tak.
ale czemu jezeli a = 2r to r nie moze sie rownac zeru ?
ale czemu jezeli a = 2r to r nie moze sie rownac zeru ?
Podstaw sobie to a do mianownika. Otrzymasz 3r i 6r w mianownikach. Jeżeli r=0 to co Ci wyjdzie w mianowniku? ;)
Hmm... Tak niestandardowe ze w zyciu bym o tym nie pomslal :)
Dzieki wielkie.

Ktoś wie jak liczymy takie cuś ? --------------------------->
y=-2x^2+12x
a) y=18
18=-2x^2+12x
0=-2x^2+12x-18
0=-x^2+6x-9
delta=36 - 4 * (-1) * (-9) = 36 - 36 = 0
czyli tylko 1 punkt wspólny dla y=18
Podstawiasz do wzoru funkcji i patrzysz co się dzieje. Jeśli otrzymasz jedno miejsce zerowe to znaczy, że w jednym punkcie się te dwie funkcje przecinają.
help plx :)
" Zbadaj liczbe rozwiazan w zaleznosci od parametru p
x^4 + (p+1)x^2 +p^2 - 1 = 0 "
Zadanie jest dla mnie po prostu zbyt abstrakcyjne...
Oczywiscie podstawiam x^2=t
wyliczam delte z rownania kwadratowego t
wychodzi mi delta z parametrem, wyliczam delte z delty (tutaj pojawia sie element ktorego nie umiem pojac moim malym rozumem, moglby to ktos jakos po ludzku wytlumaczyc ?) i wychodzi ona 64, wyliczam pierwiastki i wychodzi -1 i 10/6 ... Co z tym zrobic ? Co z podstawieniem ?
edit:
juz chyba wiem.
Jezeli rownanie kwadratowe T bedzie mialo
2 pierwiastki
- dwa dodatnie : to wielomian bedzie mial 4 rozwiazania
- jedno dodatnie jedno ujemne : to dwa rozwiazania
1 pierwiastek
- dodatni : dwa rozwiazania
Zgadza sie ?
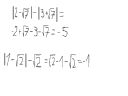
Miałem już nic o was nie pytać bo trochę was wykorzystuje. Niemniej problem na jaki natknąłem się teraz doprowadza mnie do szału, a wiem, że dla was to bułka z masłem.
Dałem 3 rozwiązania wartości bezwzględnej. Problem w tym, że za każdym razem sposób wykonywania działania jest jakiś inny i ilekroć dostaje nowy zapis coś zwalam zugerując się poprzednimi zadaniami.... Chciałbym wiedzieć czy są jakieś wzory które rządzą się tymi działaniami czy trzeba to brać jakoś na logikę ? Jeśli tak to w jaki sposób
--------------------------->
Owszem, są wzory definiujące po prostu wartość bezwzględną. Jak wyrażenie w środku jest większe/równe od zera, to wartość bezwzględną opuszczasz bez zmiany znaku, a jak jest mniejsze od zera - zmieniasz znak. Oto cała filozofia.
Tak jak w Twoich przykładach:
sqrt(7)>2, więc 2-sqrt(7)<0 więc |2-sqrt(7)|=-2+sqrt(7) --> zmieniamy znaki
3+sqrt(y)>0, więc |3+sqrt(7)|=3+sqrt(7)
itd.

Muszę w sprawozdaniu wyliczyć niepewność wielkości wyznaczanej. Wielkością tą jest powiększenie mikroskopu K. Wg. tego co zdążyłem zanotować, trzeba obliczyć pochodne cząstkowe dla tego wzoru i z tego błąd pomiaru. Nie jestem pewien tylko czy dobrze to zrobiłem. Mógłby to ktoś sprawdzić i ew. naprowadzić na dobrą drogę? :)
max_101 --> gdy liczysz pochodna wzgledem zmiennej ktora jest w mianowniku to nie mozesz tego tak pomnozyc jak 3 i 4 skladnik twojej sumy. Gdy f(x) = a/x to f'(x) = -a(x^-2)
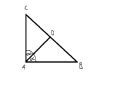
planimetria -.-
Przyprostokątne trójkąta prostkokątnego mają długości 3 i 4. Oblicz długość odcinka AD (rysunek obok).
No więc pomyślałem że jak AD dzieli kąt prosty na 2 równe części to jest to dwusieczna. Tylko nie wiem jak obliczyć ten odcinek jeśli nie tworzy a AB kąta prostego. Jakieś pomysły ?
sokrates - weź się porządnie do roboty bo w przyszłości problemy będziesz miał. Oblicz z Pitagorasa długość CB. Potem zastosuj wzór na pole trójkąta czyli podstawa*wysokość*1/2.
AD nie dzieli kąta A na dwie równe części.
Znaczy no nie mam zamiaru dyskutować bo się na tym nie znam, ale jeżeli AD dzieli kąt na 2 alfy, to znaczy, że te kąty są równe, czyli to jest dwusieczna. A dwusieczna nie stworzy z CB kąta prostego, czyli wzór na wysokość chyba odpada. No ale oczywiście mówie, noga ze mnie z matmy dlatego robie dużo żeby to poprawić. Problem w tym że teraz przez te działy tylko w szkole szybko przechodzimy i nie mam czasu analizowac każdego zadania.

Moze tak?
tomazzi -> Ale tak jest w tresci zadania, przynajmniej moim zdaniem. AD dzieli kat A na dwie rowne czesci.
Aaa, źle zrozumiałem :) Zapewne odpowiedź pajkula jest dobra.
Max_101 ---> Pamietaj jeszcze, ze przy szacowaniu bledu metoda rozniczki zupelnej dodaje sie wartosci bezwgledne pochodnych czastkowych.
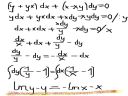
Joł matematycy :)
Znowu przyszedłem po poradę, tym razem dotyczącą równań różniczkowych :)
mianowicie miałem przykład zrobiłem go i chciałem się poradzić czy jest ok czy raczej muszę coś poprawić ->
Dobra napisze tutaj.
Problem z dwoma zadaniami.
zad.1. Suma 3 wyrazów ciągu arytmetycznego jest równa 0. Jeśli do pierwszego wyrazu dodamy 1, do drugiego dodamy 2 a od trzeciego odejmiemy 6 to otrzymamy 3 kolejne wyrazy ciagu geometrycznego. Wyznacz ciąg arytmetyczny.
No więc zrobiłem:
xyz - ciąg arytmetyczny
x+y+z=0
y-x=z-y
x+1, y+2, z-6 - ciąg geom.
(y+2)/(x+1)=(z-6)/(y+2)
Po misternych obliczeniach delta wychodzi mi -28...Więc coś chyba jest nie tak jak powinno. Czyżbym zrobił złe układy równań?
zad.2 Suma 3 wyrazów ciągu geometrycznego jest równa 6. Jeśli od ostatniego wyrazu odejmiemy 18 to otrzymamy trzy kolejne wyrazy ciagu arytmetycznego. Wyznacz wyrazy ciągu geometrycznego.
I zrobiłem:
x+y+z=6
y/x=z/y
y-x=z-18-y
Wychodzi mi delta -144 więc też coś nie tak. Any ideas?
zad.2 Suma 3 wyrazów ciągu
connor - jakie masz rownanie w 1?
mi wyszly takie dwa ciagi:
aryt -5 0 5 geom -4 2 -1
aryt -2 0 2 geom -1 2 -4
w 2 wychodzi:
g:2 -4 8 a: 2 -4 -10
g:8 -4 2 a:8 -4 -16
napisz swoje rownanie kwadratowe
W 1 zrobiłem tak:
x+y+z=0
y-x=z-y
(y+2)/(x+1)=(z-6)/(y+2)
x=0-y-z
y-x=z-y
y^2+4y+4=zx-12-6x
y-(o-y-z)=ziy
y-0+y+z=z-y
y+y+y=0
3y=0
y=0
y^2+4y-y=zx-12-6x
0^2+4*0+0=z(0-y-z)-12-6(0-y-z)
0=0-zy-z^2-12-6y-6z
0=-zy-z^2-12-6*0-6z
0=-z*0-z^2-12-6*0-6z
0=-z^2-12-6z
0+12=-z^2-6z
12=-z^2-6z
-z^2-6z-12=0
Delta na minusie i dupa...Zły układ równań może?
edit. Widze jeden błąd, w pewnym momencie zamiast 0 za y podstawiłem 4 ale to i tak nic nie zmienia bo i tak jak podstawie 0 wyjdzie delta na minusie...
komplikujesz sobie zycie
jak juz masz y to podstaw do (y+2)/(x+1)=(z-6)/(y+2) i dopiero zrob z tego rownanie, bo ze swoim cos musiales zle zrobic:)
wyjdzie ci cos w stylu:
z^2-7z+10 = 0
[173]
Jest to równanie różniczkowe zupełne pierwszego rzędu, które rozwiązuje się chyba odrobinę trudniej niż Twoim sposobem. Tutaj masz super wytłumaczony przykład: http://pl.wikipedia.org/wiki/Równanie_różniczkowe_zupełne - robisz analogicznie i po sprawie.
edit. [177]
Jak z (x+1)(z-6) wyszło Ci zx-12-6x?? Zresztą strasznie komplikujesz, tak jak napisał el.kocyk.
el kocyk--->faktycznie zrobiłem tak jak napisałeś i wyszło mi -5,0,5 i -2,0,2...Dzięki raz jeszcze ;) Jutro kartkówka, musze się przygotować...
Delta wyszła 9 i pierwiastek 3...Czyli jednak coś popierniczyłem w tamtym równaniu ;)
http://www.zadania.info/3306780
Moglby mi ktos wytlumaczyc sposob II? A konkretnie dlaczego przy drugiej racie kwota ktora splacamy wynosi x/1,03^2. W przypadku pierwszej raty nie mam zadnych watpliwosci, ale dlaczego akurat przy kolejnych ratach mianownik wzrasta 1,03 razy?
Odsetki są dopisywane kwartalnie, więc aby wszystkie raty kapitalizować na jeden moment w czasie, wartość kolejnych rat musisz aktualizować na okresy odległe o kolejno: 1 kwartał (dzielisz przez 1,03), 2 kwartały (dzielisz przez 1,03^2), 3 kwartały (dzielisz przez 1,03^3) i 4 kwartały (1,03^4).
Nic nie rozumiem, ale sprobuje jeszcze raz:
Jezeli x to ilosc pieniedzy jaka place na koniec kwartalu, ktora jest stala, to:
W 1. kwartale place 3% odsetek z niezplaconej kwoty. + kredyt
W 2. kwartale 3% odsetek z niezplaconej kwoty, ktora jest mniejsza niz w pierwszym kwartale o x/1,03. + kredyt wiekszy niz w przypadku 1 raty, bo musi byc rowny w 4 kwartalach.
W 3. kwartale 3% odsetek z niezplaconej kwoty, ktora jest mniejsza niz w 2 kwartale o... ile?
joł. natknąłem się na takie rozwiązanie zadania :
http://forum.zadania.info/viewtopic.php?f=20&t=1367 ( chodzi o drugiego posta ).
I tam jest napisane że trójąty GDC i FEC są podobne do trójkąta ABC. Obliczamy skalę podobieństa trójkątów FEC i ABC.
i tam na dole jest jakiś dziwny zapis. Zgadzam się, że FEC/ABC = 1/3, ale nie rozumiem co to jest to K i dlaczego jest do kwadratu ? Chodzi mi tylko o rozszyfrowanie tego znaku, co on oznacza ?
PS. treść do zadania w poście pierwszym, zadanie nr 2.
sokrates92 ==> k to jest skala podobieństwa tych trójkątów (po prostu takie oznaczenie sobie przyjął autor rozwiązania - zresztą dość powszechnie oznacza się skalę podobieństwa tą literką). A podniesione jest do kwadratu, ponieważ stosunek pól trójkątów podobnych jest równy kwadratowi skali podobieństwa :)
Mam tu wykres takiej funkcji, którą muszę narysować, już po przekształceniach:
http://img836.imageshack.us/i/unled1a.png/
Może mi ktoś przypomnieć jak to się robiło? Muszę rozpisać moduł i to jakoś się poskraca z mianownikiem czy co?
Tak. Musisz rozpisać moduł i skrócić co się da z mianownikiem.
Tylko że chyba w 2 przypadkach będzie, że zostanie na dole funkcja kwadratowa. Co z tym zrobić?
dla x>1 masz:
1/ (x+2)
dla -3<x<1 masz:
-1 / (x+2)
dla x<-3 masz:
1/(x+2)
Niech mnie ktoś poprawi jeżeli się mylę.
Panowie, zaraz sobie wyrwę resztkę włosów z głowy.
|5-7| - |-3+4| =?
|5-7| - |-3+4| = (5-7) - (-3+4) = 5 - 7 + 3 - 4 = 8 - 11= -3.
W książce rozwiązanie zadania to 1.
WTF?
|5-7| - |-3+4|
wartość bezwzględna nie może być ujemna, więc zmieniasz znaki.
(-5+7)-(-3+4)=2+3-4=1
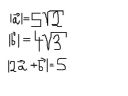
Oblicz iloczyn skalarny wektorów a i b, jeżeli: (screen)
Panowie, dostałem zaćmienia niesamowitego po tych świętach i kompletnie nie mam pomysłu. Jakaś rada?
Up.
TPU ==> Rysunek, oznaczasz co masz dane, zastanowić się, co by się przydało znać i jedziemy ;)